The Formula for the Center of a Circle

To find the coordinates (x, y) of the center of a circle from its general equation $$ x^2 + y^2 + Dx + Ey + F = 0 $$, you can use the following formula: $$ O(x, y) = \left( -\frac{D}{2}, -\frac{E}{2} \right) $$

When the equation of the circle is written in standard form

\[ (x - h)^2 + (y - k)^2 = r^2 \]

The center and radius of the circle on the Cartesian plane are much more obvious:

• \( (h, k) \) are the coordinates of the center of the circle
• \( r \) is the radius of the circle.

If the circle's equation is in general form:

\[ x^2 + y^2 + Dx + Ey + F = 0 \]

You can find the center \((h, k)\) using these formulas:

$$ h = -\frac{D}{2} $$

$$ k = -\frac{E}{2} $$

In these formulas, \(D\) and \(E\) are the coefficients of the \(x\) and \(y\) terms in the general equation $ x^2 + y^2 + Dx + Ey + F = 0 $ of the circle.

Therefore, the center of the circle is given by the coordinates \((-D/2, -E/2)\).

Note: Alternatively, you can find the coordinates of the center by transforming the general equation of the circle $ x^2 + y^2 + Dx + Ey + F = 0 $ into the standard form $ (x - h)^2 + (y - k)^2 = r^2 $ by completing the square and adding the necessary terms.

An Example

Let's go through a practical example to clarify the process.

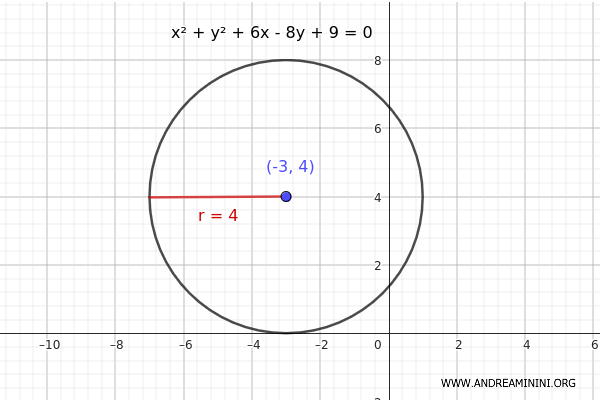
Given the general equation of a circle:

\[ x^2 + y^2 + 6x - 8y + 9 = 0 \]

To find the center of the circle, identify the coefficients \(D\) and \(E\) in the equation. In this case, they are:

$$ D = 6 $$

$$ E = -8 $$

Use the formulas to find the coordinates \(h\) and \(k\) of the center of the circle:

$$ h = -\frac{D}{2} = -\frac{6}{2} = -3 $$

$$ k = -\frac{E}{2} = -\frac{-8}{2} = 4 $$

Therefore, the center of the circle is \((-3, 4)\).

The Proof

To demonstrate how to derive the center of the circle from the general equation \( x^2 + y^2 + Dx + Ey + F = 0 \), we need to transform the equation into the standard form \((x - h)^2 + (y - k)^2 = r^2\).

Consider the general equation of a circle:

$$ x^2 + y^2 + Dx + Ey + F = 0 $$

Group the \(x\) and \(y\) terms:

$$ (x^2 + Dx) + (y^2 + Ey) + F = 0 $$

Complete the square for the \(x\) terms by adding and subtracting $ \left(\frac{D}{2}\right)^2 $:

$$ (x^2 + Dx + \left(\frac{D}{2}\right)^2) - \left(\frac{D}{2}\right)^2 + (y^2 + Ey) + F = 0 $$

$$ (x + \frac{D}{2})^2 - \left(\frac{D}{2}\right)^2 + (y^2 + Ey) + F = 0 $$

Complete the square for the \(y\) terms by adding and subtracting $ \left(\frac{E}{2}\right)^2 $:

$$ \left(x + \frac{D}{2}\right)^2 - \left(\frac{D}{2}\right)^2 + (y^2 + Ey + \left(\frac{E}{2}\right)^2) - \left(\frac{E}{2}\right)^2 + F = 0 $$

$$ \left(x + \frac{D}{2}\right)^2 - \left(\frac{D}{2}\right)^2 + \left(y + \frac{E}{2}\right)^2 - \left(\frac{E}{2}\right)^2 + F = 0 $$

Reorganize the terms:

$$ \left(x + \frac{D}{2}\right)^2 + \left(y + \frac{E}{2}\right)^2 = \left(\frac{D}{2}\right)^2 + \left(\frac{E}{2}\right)^2 - F $$

This gives the standard equation of the circle \((x - h)^2 + (y - k)^2 = r^2\), where:

$$ h = -\frac{D}{2} $$

$$ k = -\frac{E}{2} $$

Therefore, the center of the circle \((h, k)\) is:

$$ \left(-\frac{D}{2}, -\frac{E}{2}\right) $$

And the radius \(r\) is:

$$ r = \sqrt{\left(\frac{D}{2}\right)^2 + \left(\frac{E}{2}\right)^2 - F} $$

This proves the formula for finding the center and radius of a circle when the equation is in general form.

And so on.