Pencil of Circles

A pencil of circles is a collection of circles that share certain common properties.

There are primarily two types: proper pencils and improper pencils.

• Proper Pencil
  All circles pass through two fixed points, known as base points. The general equation of a proper pencil is \( \lambda (x^2 + y^2) + \mu (Ax + By + C) = 0 \), where \( \lambda \) and \( \mu \) are parameters.
• Improper Pencil
  All circles have the same center and differ only in radius. The equation of an improper pencil is \( (x - h)^2 + (y - k)^2 = r^2 \), with \( (h, k) \) as the common center and \( r \) varying.

Pencil of Circles from Two Generating Circles

A pencil of circles is the set of all circles formed by the linear combination of two generating circles. $$ (x^2 + y^2 + ax + by + c) + k \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$ where k is any integer value.

This equation generates all circles in the pencil as the parameter k varies, except for the second generating circle, since no value of k can reproduce it.

However, there are two special cases worth examining in detail.

• If k=0, you get the first circle: $$ (x^2 + y^2 + ax + by + c) + k \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$ $$ (x^2 + y^2 + ax + by + c) + 0 \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$ $$ x^2 + y^2 + ax + by + c = 0 $$
• If k=-1, you get a line called the radical axis of the pencil of circles: $$ (x^2 + y^2 + ax + by + c) + k \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$ $$ (x^2 + y^2 + ax + by + c) + (-1) \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$ $$ \require{cancel} \cancel{x^2} + \cancel{y^2} + ax + by + c - \cancel{x^2} - \cancel{y^2} - a'x - b'y - c' = 0 $$ $$ (a - a')x + (b - b')y + (c - c') = 0 $$

Note: The radical axis of the pencil of circles is considered a "degenerate circle" because it can be thought of as a circle with an infinite radius.

The radical axis of the pencil of circles can either intersect or not intersect the two generating circles.

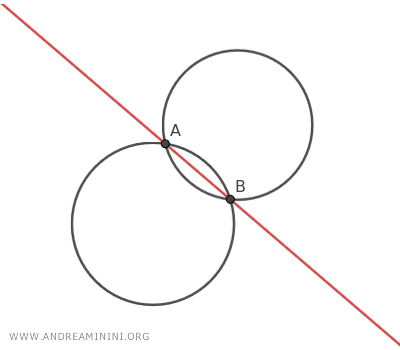
• If the generating circles intersect at two points A and B, called the base points of the pencil, the radical axis passes through both points.
  
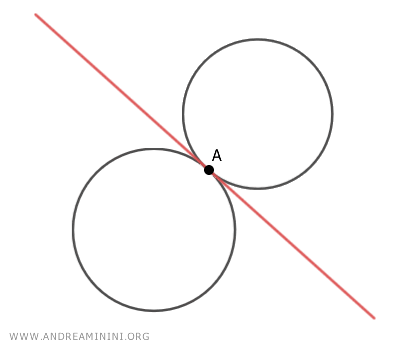
• If the generating circles are tangent at a single base point A, the radical axis passes through the point of tangency of the two generating circles.
  
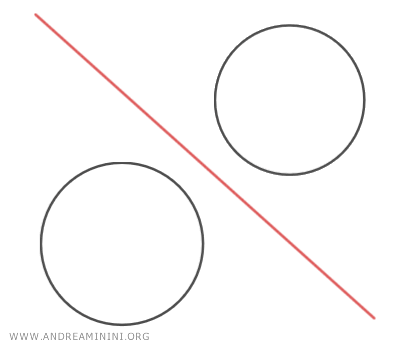
• If the generating circles are external, meaning they do not share any points, the radical axis passes through the external space between the two generating circles.
  

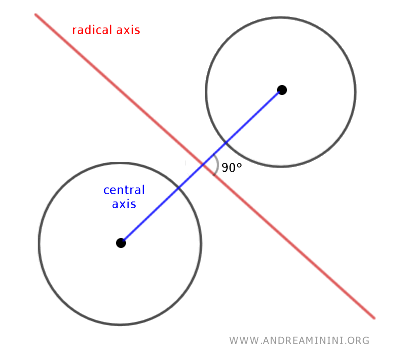
The collection of all the centers of the circles generated in a pencil of circles forms an axis perpendicular to the radical axis, known as the central axis of pencil.

Note: In the special case where the coefficients a=a' and b=b' are equal, the two generating circles are concentric. In this case, the pencil of circles consists solely of concentric circles, and the radical axis does not exist.

Example

Consider two generating circles:

$$ C_1 : \ x^2 + y^2 + 2x + 3y - 5 = 0 $$

$$ C_2 : \ x^2 + y^2 - 4x - 4y + 1 = 0 $$

These two circles intersect at two base points A and B.

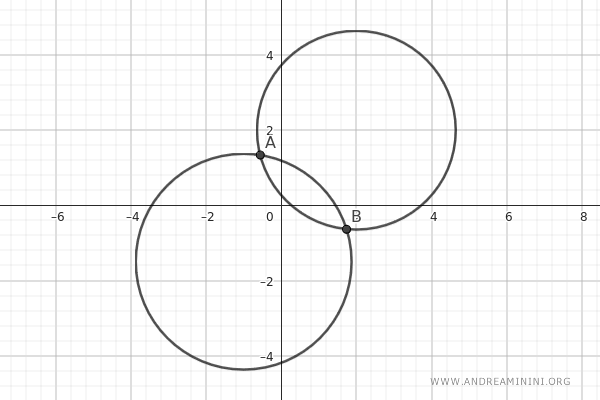
This means that all circles in the pencil will pass through these two points A and B.

The equation of the pencil of circles from the two generating circles is as follows:

$$ C_1 + k \cdot C_2 = 0 $$

$$ (x^2 + y^2 + 2x + 3y - 5) + k \cdot (x^2 + y^2 - 4x - 4y + 1) = 0 $$

As the parameter k varies, I obtain all the circles in the pencil.

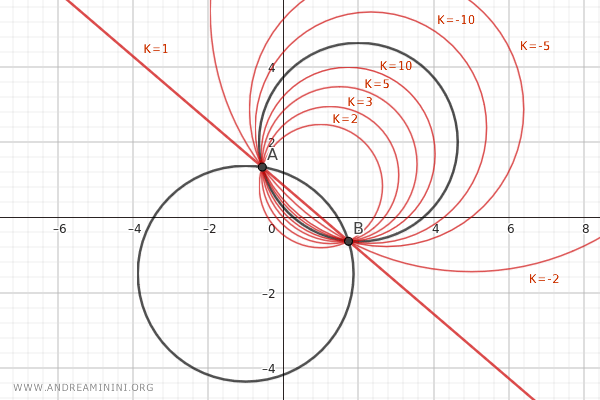
When k=0, you get the circle C₁:

$$ (x^2 + y^2 + 2x + 3y - 5) + 0 \cdot (x^2 + y^2 - 4x - 4y + 1) = 0 $$

$$ x^2 + y^2 + 2x + 3y - 5 = 0 $$

When k=-1, you get the radical axis of the circles, which passes through both base points A and B of the pencil of circles:

$$ (x^2 + y^2 + 2x + 3y - 5) + (-1) \cdot (x^2 + y^2 - 4x - 4y + 1) = 0 $$

$$ \require{cancel} \cancel{x^2} + \cancel{y^2} + 2x + 3y - 5 - \cancel{x^2} - \cancel{y^2} + 4x + 4y - 1 = 0 $$

$$ (2 + 4)x + (3 + 4)y - 5 - 1 = 0 $$ $$ 6x + 7y - 6 = 0 $$

The central axis of a pencil of circles is the line that passes through all the centers of the circles in the pencil and is perpendicular to the radical axis.

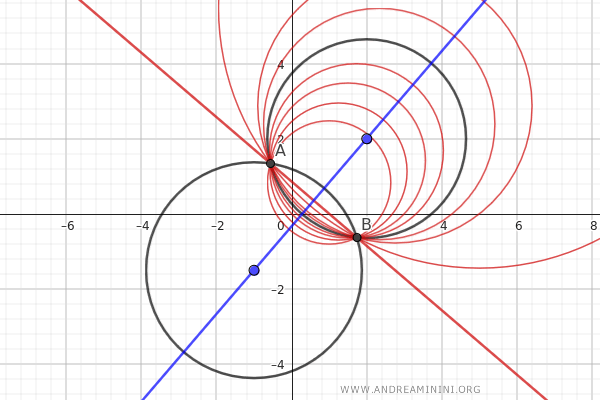
The Proof

Consider two generating circles:

$$ C_1 = x^2 + y^2 + ax + by + c = 0 $$

$$ C_2 = x^2 + y^2 + a'x + b'y + c' = 0 $$

Calculate the linear combination of the two circles where h and j are any integers:

$$ h \cdot C_1 + j \cdot C_2 = 0 $$

$$ h \cdot (x^2 + y^2 + ax + by + c) + j \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$

This equation allows me to obtain all the circles in the pencil of lines as the coefficients h and j vary.

Note: If h=0 and j=1, you get the equation C₂. Conversely, if h=1 and j=0, you get the circle C₁.

Divide both sides of the equation by h:

$$ \frac{1}{h} \cdot [ h \cdot (x^2 + y^2 + ax + by + c) + j \cdot (x^2 + y^2 + a'x + b'y + c') ] = 0 \cdot \frac{1}{h} $$

$$ (x^2 + y^2 + ax + by + c) + \frac{j}{h} \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$

Let k be the ratio j/h:

$$ (x^2 + y^2 + ax + by + c) + k \cdot (x^2 + y^2 + a'x + b'y + c') = 0 $$

In this way, by varying k, I can obtain all the circles in the pencil of lines, except for the circle C₂.

Note: If k=0, you get the equation C₁. Conversely, in this form of the pencil of circles, there is no value of the parameter k that can generate the circle C₂.

And so on.