Inscribed angle
An inscribed angle forms when two lines originating from any two points on a circle’s circumference meet at a point on that circumference, creating a convex angle. These lines can either both cut across the circle or one can cut across while the other lies tangent to it.
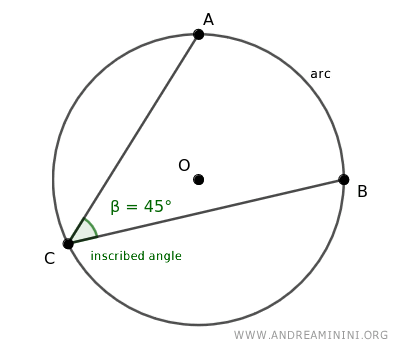
This angle's arms intersect the circle at two separate points, marking the ends of an arc.
This setup allows us to say that the inscribed angle subtends the arc, or in other words, the arc is subtended by the angle.
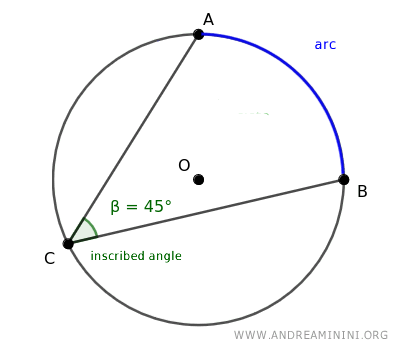
For any given arc AB on the circle, an infinite number of inscribed angles can be drawn with their arms intersecting at points A and B.
A handy reminder: all inscribed angles subtending the same arc share the same angular measure.
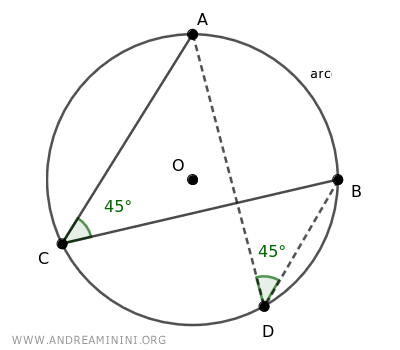
Example: Take arc AB and consider two inscribed angles subtending this arc. Both angles will share the same measure, hence are congruent.
An inscribed angle β and a central angle α are termed corresponding angles when they subtend the same arc.
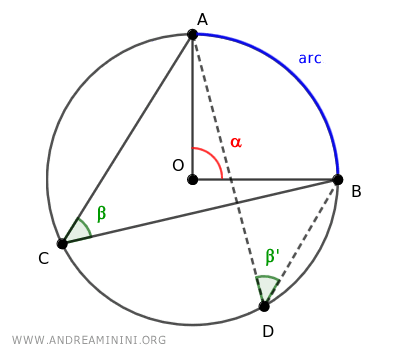
A unique central angle (α) and an infinite array of inscribed angles (β, β') can subtend an arc.
Also, each inscribed angle measures exactly half of the central angle subtending the same arc.
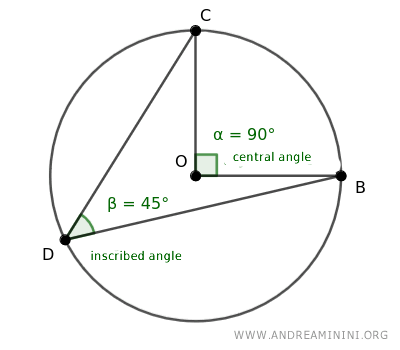
Therefore, every one of the countless inscribed angles subtending the same arc are congruent (β≅β'), that is, they are of equal measure.
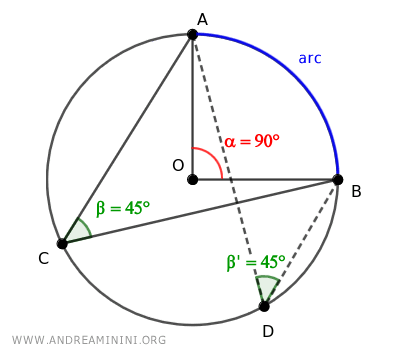
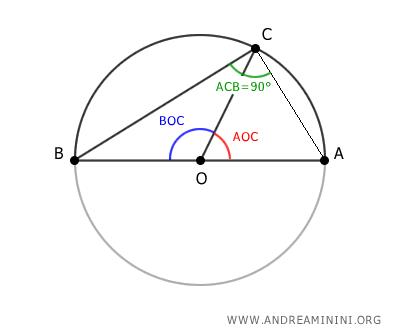
Thus, by the Inscribed Angle Theorem, any inscribed angle that subtends a semicircle is invariably a right angle (90°).
Observations
A few more insights on inscribed angles:
- Given an arc, all inscribed angles that subtend this arc are congruent, meaning they have the same angular measure.
- The measure of an inscribed angle is half that of the arc it subtends.
- Exceptions to inscribed angles: Not all angles qualify as inscribed angles. For instance, angle α does not have a side that cuts across or lies tangent to the circle, and angle β is not convex.
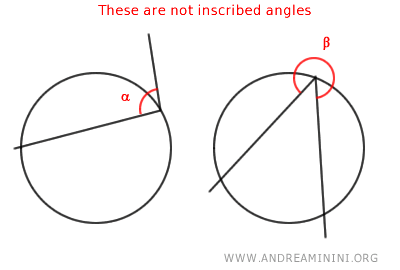
And so forth.
