Theorem of Central and Inscribed Angles

In a circle, the inscribed angles α have a measure equal to half of the corresponding central angle β that subtends the same arc AB. $$ \alpha = \frac{1}{2} \beta $$ Example:

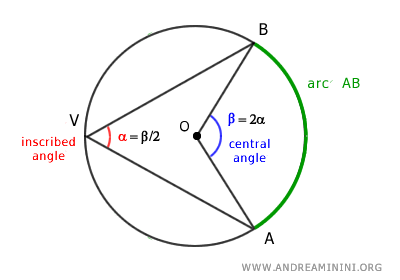
Alternatively, we can say that the central angles β are twice the measure of their corresponding inscribed angles α.

$$ \beta = 2 \alpha $$

Since there is only one central angle but an infinite number of inscribed angles subtending the same arc AB, we can deduce that all inscribed angles α subtending the same arc AB are congruent to each other.

 

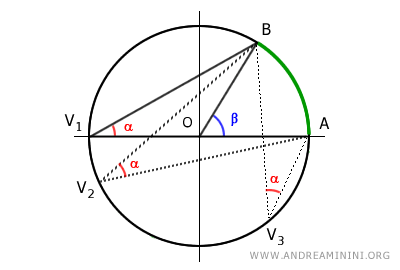
Additionally, if an inscribed angle subtends a semicircle, it is a right angle (90°) because, in this case, the central angle is a straight angle (180°).

Proof

To prove this theorem, we need to consider three cases: when the center of the circle O lies on a side, inside, or outside the inscribed angle.

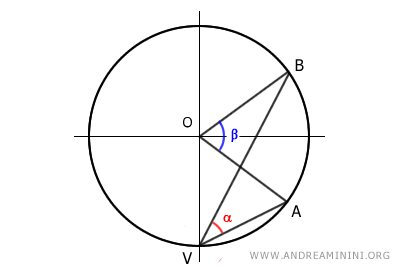
A] The center lies on a side of the inscribed angle

If the center O of the circle lies on a side of the inscribed angle α, then this side (AV) is a diameter of the circle.

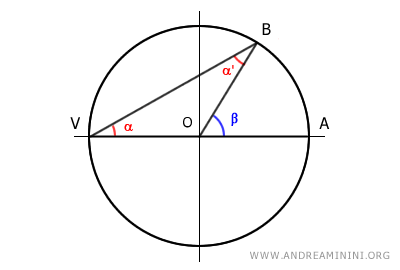
Since AV is a diameter, its half OV is a radius of the circle.

In this case, triangle VBO is an isosceles triangle because it has two equal sides, which are the radii OV ≅ OB.

Knowing that an isosceles triangle has congruent base angles, we deduce that the angles α ≅ α' are congruent.

$$ \alpha = \alpha' $$

According to the exterior angle theorem, the central angle β is an exterior angle of triangle VBO and is equal to the sum of the non-adjacent interior angles α + α'

$$ \beta = \alpha + \alpha' $$

Since α ≅ α' are congruent, we can write α + α' = 2α

Therefore, the central angle (β) is twice the inscribed angle (2α)

$$ \beta = 2 \alpha $$

Consequently, the inscribed angle (α) is half of the central angle (β/2).

$$ \alpha = \frac{1}{2} \beta $$

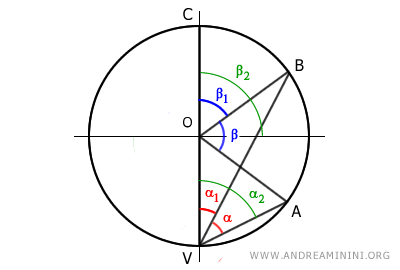
B] The center lies inside the inscribed angle

In this case, the center O of the circle lies inside the inscribed angle α.

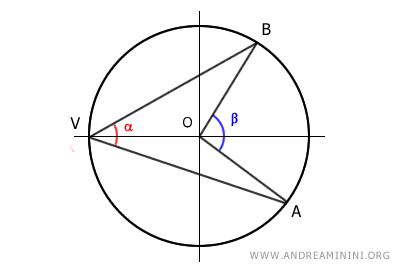
Draw the diameter VC to split the inscribed angle α and the central angle β into two parts.

Now the inscribed and central angles are as follows:

$$ \alpha = \alpha_1 + \alpha_2 $$

$$ \beta = \beta_1 + \beta_2 $$

This way, both inscribed angles α₁ and α₂ have one side that coincides with the diameter of the circle.

In section [A] of this proof, we have already demonstrated that inscribed angles with one side coinciding with the diameter have a measure equal to half of the corresponding central angles.

Therefore, the inscribed angles α₁ and α₂ are half the measures of their corresponding central angles β₁ and β₂

$$ \alpha_1 = \frac{1}{2} \beta_1 $$

$$ \alpha_2 = \frac{1}{2} \beta_2 $$

Knowing that the inscribed angle is the sum of the angles α = α₁ + α₂

$$ \alpha = \alpha_1 + \alpha_2 $$

Substitute α₁ = (1/2)β₁ and α₂ = (1/2)β₂

$$ \alpha = \frac{1}{2} \beta_1 + \frac{1}{2} \beta_2 $$

$$ \alpha = \frac{1}{2} \cdot ( \beta_1 + \beta_2 ) $$

Finally, since the central angle is the sum of the angles β = β₁ + β₂

$$ \alpha = \frac{1}{2} \cdot \beta $$

This shows that the inscribed angle (α) is half of the central angle (β/2).

Consequently, the central angle (β) is twice the inscribed angle (2α).

$$ \beta = 2 \alpha $$

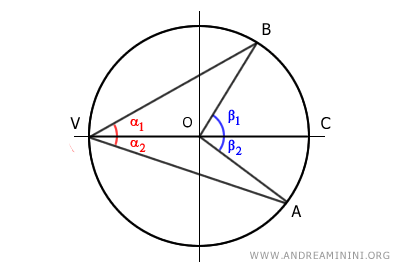
C] The center lies outside the inscribed angle

Lastly, we need to examine the case where the center O of the circle lies outside the inscribed angle α.

Draw the diameter VC to obtain two other angles that are related to the angles α and β by construction.

 

By construction, the inscribed angle is α = α₂ - α₁, while the central angle is β = β₂ - β₁

$$ \alpha = \alpha_2 - \alpha_1 $$

$$ \beta = \beta_2 - \beta_1 $$

The angle α₁ is an inscribed angle with one side as a diameter (VC) of the circle. As demonstrated in section [A], its measure is half of the corresponding central angle β₁

$$ \alpha_1 = \frac{1}{2} \beta_1 $$

The angle α₂ is also an inscribed angle with one side as a diameter (VC) of the circle. For the same reason, its measure is half of the corresponding central angle β₂

$$ \alpha_2 = \frac{1}{2} \beta_2 $$

Knowing α₁ = β₁/2 and α₂ = β₂/2, substitute them into the equation α = α₂ - α₁

$$ \alpha = \alpha_2 - \alpha_1 $$

$$ \alpha = \frac{1}{2} \beta_2 - \frac{1}{2} \beta_1 $$

$$ \alpha = \frac{1}{2} \cdot ( \beta_2 - \beta_1 ) $$

Knowing that the central angle is the difference β = β₂ - β₁

$$ \alpha = \frac{1}{2} \cdot \beta $$

This shows that the inscribed angle (α) is half of the central angle (β/2).

Consequently, the central angle (β) is twice the inscribed angle (2α).

$$ \beta = 2 \alpha $$

In conclusion, the theorem is proven for all possible cases.

And so on.