Circle Equation in Polar Form
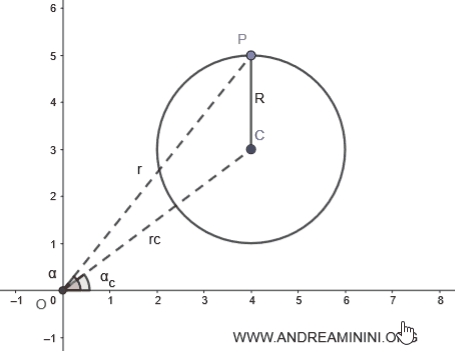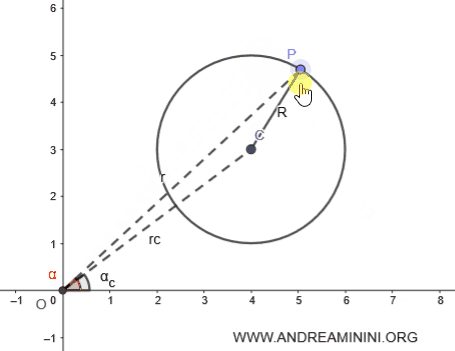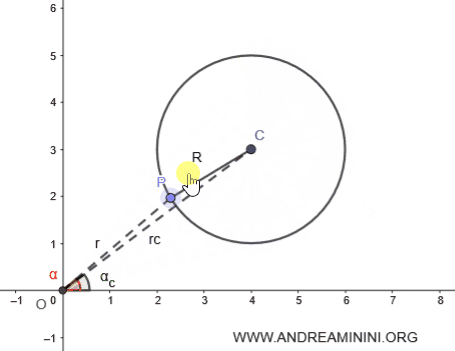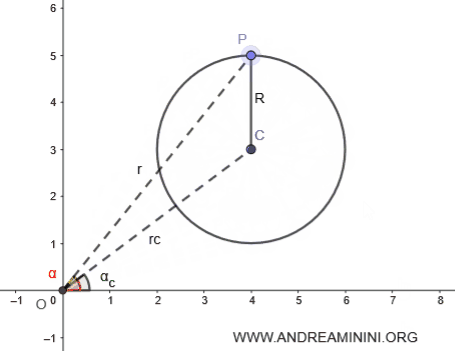
The polar form of the circle equation is expressed as: $$ r^2 + r_c^2 - 2 \cdot r \cdot r_c \cos (\alpha - \alpha_c) - R^2 = 0 $$ where \( R \) is the radius of the circle, and \( r_c \) and \( r \) represent the distances from the origin (pole) to the center \( C \) and to any point \( P \) on the circle, respectively.
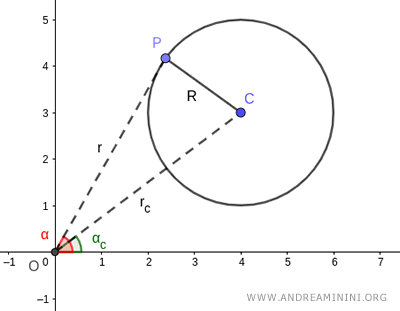
By varying the polar coordinates (α, r), all the points on the circle can be determined.
Here, the angle α and the segment length r serve as the variables.
Proof
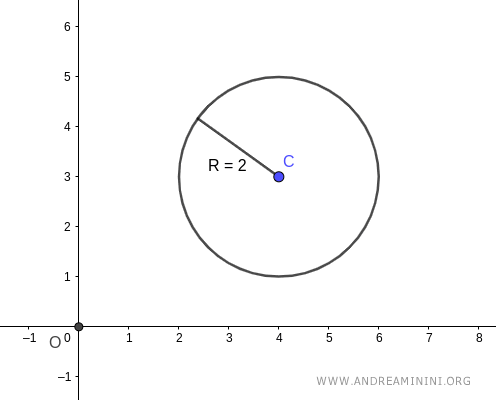
Consider any circle on the plane.
The circle has a radius of \( R = 2 \).
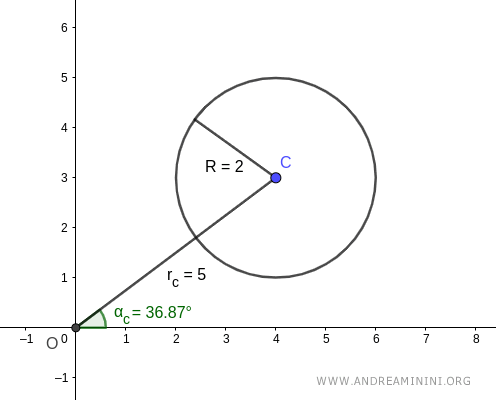
The center of the circle \( C \) is located at the polar coordinates (αc, rc).
$$ C: (\alpha_c, r_c) = (36.87°, 5) $$
Here, the angle αc = 36.87° and the segment \( r_c \) = 5.
Now, take any point \( P \) on the circle.
$$ P: (\alpha, r) = (60.27°, 4.8) $$
Point \( P \) has polar coordinates α = 60.27° and \( r \) = 4.8.
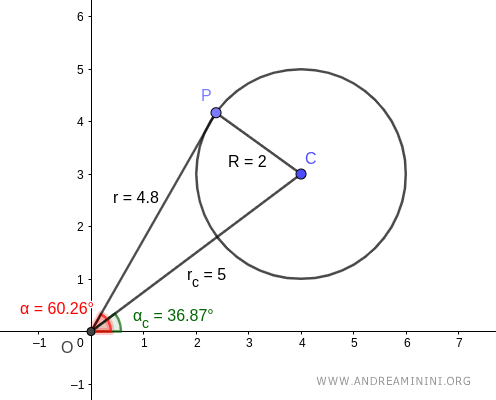
The radius \( R \), along with segments \( OP \) and \( OC \), forms triangle \( OPC \).
Applying the cosine rule to triangle \( OPC \), we get:
$$ \overline{PC}^2 = \overline{OP}^2 + \overline{OC}^2 - 2 \cdot \overline{OP} \cdot \overline{OC} \cdot \cos(\alpha - \alpha_c) $$
Given that the sides of the triangle are \( PC = R \), \( OC = r_c \), and \( OP = r \), we have:
$$ R^2 = r^2 + r_c^2 - 2 \cdot r \cdot r_c \cdot \cos(\alpha - \alpha_c) $$
Rearranging the terms, we arrive at:
$$ r^2 + r_c^2 - 2 \cdot r \cdot r_c \cdot \cos(\alpha - \alpha_c) - R^2 = 0 $$
This is the final form of the circle's equation in polar coordinates, which completes our proof.
Verification: By substituting the polar coordinate values α = 60.27°, αc = 36.87°, \( r = 4.8 \), \( r_c = 5 \), and \( R = 2 \) into the equation, we confirm that: $$ R^2 = r^2 + r_c^2 - 2 \cdot r \cdot r_c \cdot \cos(\alpha - \alpha_c) $$ $$ 5^2 = 4.8^2 + 5^2 - 2 \cdot 4.8 \cdot 5 \cdot \cos(60.27° - 36.87°) $$ $$ 25 = 23.04 + 25 - 2 \cdot 24 \cdot \cos(23.4°) $$ $$ 25 = 48 - 44 $$ $$ 25 = 25 $$ This verifies the equation is correct.
And so on.
