Power of a Point Relative to a Circle

The power of a point P(x,y) relative to a circle \( (x - a)^2 + (y - b)^2 = r^2 \) is the difference between the square of the distance from the point to the center C(a,b) of the circle and the square of the radius. $$ \pi(P) = d^2 - r^2 $$

Given that the distance d between two points is calculated using the formula

$$ d = \sqrt{((x - a)^2 + (y - b)^2)} $$

The power of the point relative to the circle is calculated using this formula

$$ \pi(P) = (x - a)^2 + (y - b)^2 - r^2 $$

This value measures the "relative" distance of the point from the circle.

Note: It does not measure the Euclidean distance from the point to the circle because it also considers the radius of the circle.

The sign of the power indicates the position of point P relative to the circle:

• If \(\pi(P) > 0\), the point is outside the circle.
• If \(\pi(P) = 0\), the point is on the circle.
• If \(\pi(P) < 0\), the point is inside the circle.

A Practical Example

Consider a point P(6,3) and a circle with center C(3,3) and radius r=2.

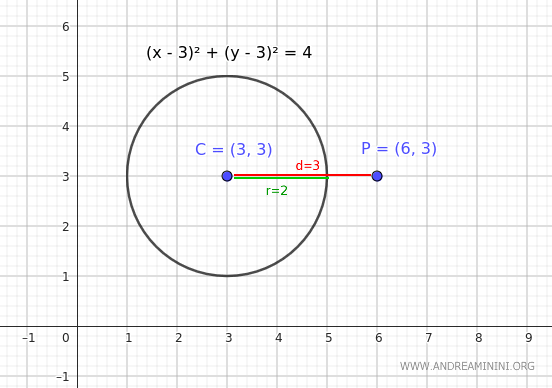
The distance from point P to the center C of the circle is easily calculated to be 3.

$$ d = \sqrt{((6 - 3)^2 + (3 - 3)^2)} = \sqrt{3^2} $$

$$ d = 3 $$

Therefore, the power of point P relative to the circle is the difference between the squares of the distance and the radius:

$$ \pi(P) = d^2 - r^2 $$

$$ \pi(P) = 3^2 - 2^2 $$

$$ \pi(P) = 9 - 4 $$

$$ \pi(P) = 5 $$

In this case, the power of the point is 5.

Example 2

Consider a point P(7,6) and the same circle from the previous example, with center C(3,3) and radius r=2.

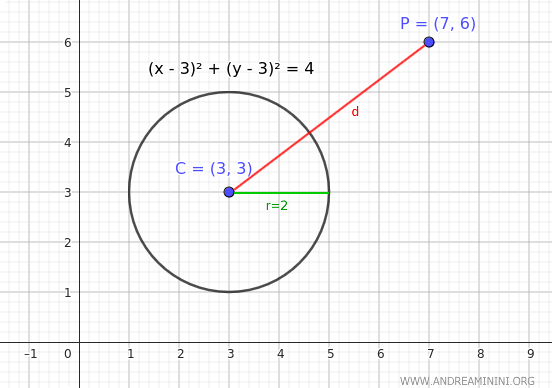
In this case, the point is farther away compared to the previous example, but the circle's radius remains the same.

Calculate the distance between the center of the circle and point P:

$$ d = \sqrt{((x - a)^2 + (y - b)^2)} $$

$$ d = \sqrt{((7 - 3)^2 + (6 - 3)^2)} $$

$$ d = \sqrt{(4^2 + 3^2)} $$

$$ d = \sqrt{(16 + 9)} $$

$$ d = \sqrt{25} $$

$$ d = 5 $$

Knowing that the radius of the circle is r=2, calculate the power of point P relative to the circle:

$$ \pi(P) = d^2 - r^2 $$

$$ \pi(P) = 5^2 - 2^2 $$

$$ \pi(P) = 25 - 4 $$

$$ \pi(P) = 21 $$

The power of the point relative to the circle is 21.

Observations

Some additional notes on the power of a point relative to a circle:

• A point P with the same power relative to two circles lies on the radical axis
  If we consider two circles with centers \(C_1\) and \(C_2\) and radii \(r_1\) and \(r_2\), a point \(P\) that has the same power relative to both circles satisfies the equation: \[ (x - x_1)^2 + (y - y_1)^2 - r_1^2 = (x - x_2)^2 + (y - y_2)^2 - r_2^2 \] This point lies on a line called the "radical axis," where the powers relative to the two circles are equal, regardless of the physical distances.
• A point P that lies on the radical axis is closer to the center of the circle with the smaller radius
  This can be easily deduced from the equation \[ (x - x_1)^2 + (y - y_1)^2 - r_1^2 = (x - x_2)^2 + (y - y_2)^2 - r_2^2 \] If one side has a smaller radius, the distance between the point and the center of that circle must also be smaller to maintain equality with the other side of the equation, thus having the same power as the other circle. $$ \pi_1(P) = \pi_2(P) $$ $$ (x - x_1)^2 + (y - y_1)^2 - r_1^2 = (x - x_2)^2 + (y - y_2)^2 - r_2^2 $$ $$ \pi_1(P) = \pi_2(P) $$ $$ (x - x_1)^2 + (y - y_1)^2 - [r_1^2 - \Delta r + \Delta r] = (x - x_2)^2 + (y - y_2)^2 - r_2^2 $$ $$ (x - x_1)^2 + (y - y_1)^2 - \Delta r - [r_1^2 - \Delta r] = (x - x_2)^2 + (y - y_2)^2 - r_2^2 $$ $$ [ (x - x_1)^2 + (y - y_1)^2 - \Delta r ] - [r_1^2 - \Delta r] = (x - x_2)^2 + (y - y_2)^2 - r_2^2 $$

Example. Consider a circle with center at C(3,3) and radius r=2 and a point P(6,3). We have already calculated the power of this point relative to the circle as $ \pi(P)=5 $. To find another circle with the same power but with a radius r=1, we can use the power formula $$ \pi(P) = d^2 - r^2 $$ In this case, we know the power of point P relative to the first circle $ \pi = 5 $ and the radius $ r=1 $ of the new circle $$ 5 = d^2 - 1^2 $$ So, the new circle must be at a distance of \(\sqrt{6}\)=2.4495 from point P $$ d^2 = 5+1 $$ $$ d = \sqrt{6} $$ In conclusion, the new circle has a smaller radius, and to have the same power, it must also have a smaller distance.

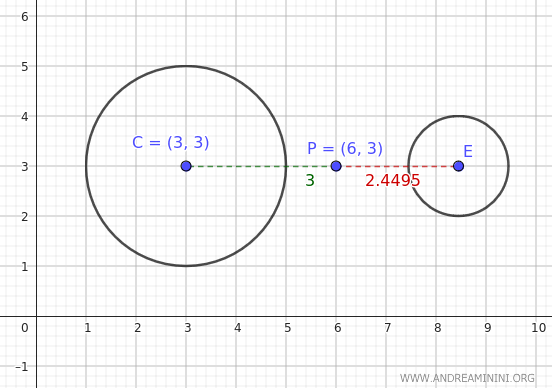
As a final check, calculate the power of point P(6,3) relative to the new circle with radius r=1 and distance d=√6 from point P, hence its center is at E(6+√6,3). $$ \pi(P) = d^2 - r^2 $$ $$ \pi(P) = (\sqrt{6})^2 - 1^2 $$ $$ \pi(P) = 6 - 1 $$ $$ \pi(P) = 5 $$ The point P has the same power \(\pi(P)=5\) relative to the new circle as well.

And so on.