Tangent Line to a Circle
A line is termed a tangent line to a circle if it intersects the circle at precisely one point.
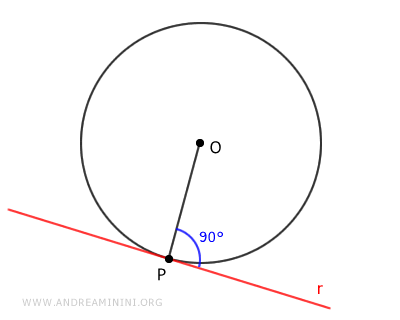
Put simply, a tangent line has a single point of contact with the circle.
This is in stark contrast to secant lines, which cross the circle at two points, and external lines, which do not intersect the circle at all.
Note: According to the theorem on intersections between a line and a circle, a line can cut through a circle at most at two points.
Uniqueness of the Tangent Line at a Circle's Point
For every point P on the circle, there exists exactly one tangent line.
This theorem underscores a critical principle: At any specific point P on the circle, there is a unique tangent line.
Demonstration
Consider a circle centered at O with radius OP. Now, think about a line (r) tangent to the circle exactly at point P.
By definition, the tangent line intersects with the circle at only this singular point.
Given that at any point on a line there can be only one perpendicular drawn, it logically follows that the tangent line at point P can have only one perpendicular.
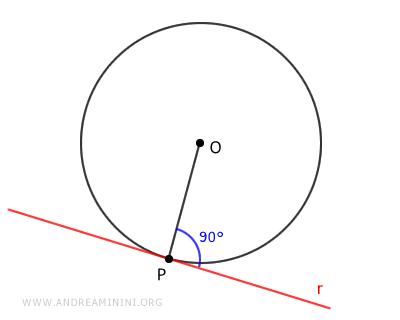
As per the theorem regarding the distance of a line from the center of a circle, if a line is tangent at a circle's point, then its distance d(r,O) from the circle's center (O) equals the radius (OP).
$$ d(r,O) \cong \overline{OP} $$
Note: When we talk about the "distance" of a line (r) from a point (O), we're referring to the shortest segment connecting them. Naturally, any other segment that is not perpendicular to the line would result in a longer path from point O to the line r.
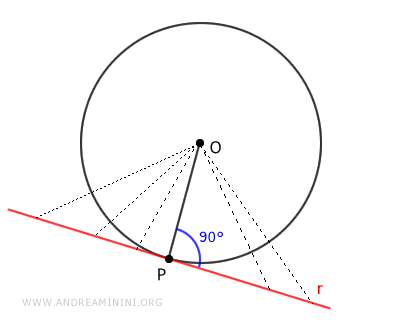
Given that the distance between a line and a point is invariably perpendicular to the line, we can deduce that the radius is perpendicular to the tangent line at point P as well.
$$ \overline{OP} \perp r $$
Since no other perpendicular lines can exist at point P on line r, it's clear that at point P on the circle, there is only one possible tangent line.
Finding the Equation of a Tangent Line Through a Point
In analytic geometry, to find the equation of a tangent line that passes through a point P(x0, y0), either on or outside a circle, we set up a system of equations:
$$ \begin{cases} x^2 + y^2 + ax + by + c = 0 \\ \\ y - y_0 = m (x - x_0) \end{cases} $$
The first equation represents the circle.
The second equation represents a line passing through the point P(x0, y0).
Next, we solve for y in the line equation and substitute it into the circle's equation:
$$ \begin{cases} x^2 + [m(x - x_0) + y_0]^2 + ax + b[m(x - x_0) + y_0] + c = 0 \\ \\ y = m(x - x_0) + y_0 \end{cases} $$
Then we solve the resulting equation for the slope m, using the condition Δ = 0, known as the tangency condition.
$$ \Delta = b^2 - 4ac $$
Here, a, b, and c are the coefficients of the quadratic equation.
Note: The tangency condition b2 - 4ac = 0 ensures that the line touches the circle at exactly one point, confirming it as a tangent. If this condition isn't met, the line either intersects the circle at two points or doesn't touch it at all.
Once we find the solution for "m," there are two possible scenarios:
- If the point P(x0, y0) is on the circle, there will be a single value of the slope m, determining the unique tangent line.
- If the point P(x0, y0) is outside the circle, there will be two values, m1 and m2, for the slope, because two tangent lines can be drawn from an external point to a circle.
Example
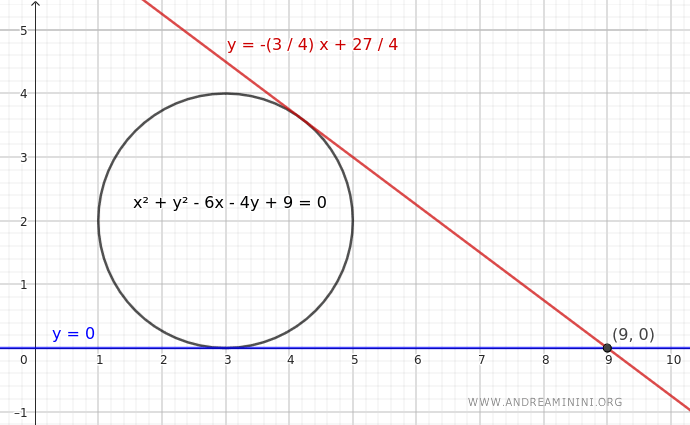
Consider a circle defined by the following quadratic equation:
$$ x^2 + y^2 - 6x - 4y + 9 = 0 $$
We need to find the tangent line(s) passing through the point P(9, 0).
First, we need to determine whether the point is on the circle or not.
We set up the system with the given circle equation and the general line equation:
$$ \begin{cases} x^2 + y^2 - 6x - 4y + 9 = 0 \\ \\ y - y_0 = m(x - x_0) \end{cases} $$
Since the line passes through P(9, 0), we substitute the coordinates x0 = 9 and y0 = 0:
$$ \begin{cases} x^2 + y^2 - 6x - 4y + 9 = 0 \\ \\ y = m(x - 9) \end{cases} $$
Next, we solve for y in the line equation and substitute this expression into the circle's equation:
$$ \begin{cases} x^2 + (mx - 9m)^2 - 6x - 4(mx - 9m) + 9 = 0 \\ \\ y = m(x - 9) \end{cases} $$
$$ \begin{cases} x^2 + m^2x^2 - 18m^2x + 81m^2 - 6x - 4mx + 36m + 9 = 0 \\ \\ y = m(x - 9) \end{cases} $$
We rewrite the quadratic equation in standard form:
$$ \begin{cases} x^2(1 + m^2) + x(-18m^2 - 6 - 4m) + 81m^2 + 36m + 9 = 0 \\ \\ y = m(x - 9) \end{cases} $$
We then apply the tangency condition by setting the discriminant of the quadratic equation to zero:
$$ \Delta = b^2 - 4ac = 0 $$
In this case, the coefficients of the quadratic equation are a = 1 + m2, b = -18m2 - 6 - 4m, and c = 81m2 + 36m + 9.
$$ \Delta = (-18m^2 - 6 - 4m)^2 - 4(1 + m^2)(81m^2 + 36m + 9) $$
$$ \Delta = (-18m^2 - 6 - 4m)^2 - 4(1 + m^2)(81m^2 + 36m + 9) $$
$$ \Delta = 324m^4 + 144m^3 + 232m^2 + 48m + 36 - 4(81m^4 + 36m^3 + 90m^2 + 36m + 9) $$
$$ \Delta = 324m^4 + 144m^3 + 232m^2 + 48m + 36 - 324m^4 - 144m^3 - 360m^2 - 144m - 36 $$
$$ \Delta = -128m^2 - 96m $$
We solve the discriminant equation:
$$ \Delta = m(-128m - 96) $$
$$ \Delta = 32m(-4m - 3) $$
The solutions to the equation are:
$$ m = 0 $$
$$ -4m - 3 = 0 $$
Thus,
$$ m = 0 $$
$$ m = -\frac{3}{4} $$
The slopes of the tangent lines passing through the point P(9, 0) are:
$$ m_1 = 0 $$
$$ m_2 = -\frac{3}{4} $$
Now we find the equations of the tangent lines.
For \(m = 0\):
$$ y = 0 $$
For \(m = -\frac{3}{4}\):
$$ y = -\frac{3}{4}(x - 9) $$
$$ y = -\frac{3}{4}x + \frac{3 \cdot 9}{4} $$
$$ y = -\frac{3}{4}x + \frac{27}{4} $$
Therefore, the equations of the tangent lines are:
$$ y = 0 $$
$$ y = -\frac{3}{4}x + \frac{27}{4} $$
These are the tangent lines to the circle passing through the point P(9, 0).
Alternative Methods for Finding Tangent Line Equations
Here are some additional methods to determine the equations of tangent lines to a circle.
- Method Using the Distance Between the Line and the Circle's Center
- The Tangent Line Method Perpendicular to the Radius
- The Tangent Line Formula Method
Method Using the Distance Between the Line and the Circle's Center
This method relies on the coordinates of the circle's center C and the radius length r.
First, I write the equation of the family of lines passing through point P(x0, y0), which can be a point on the circle or any external point.
$$ y - y_0 = m(x-x_0) $$
Then, I find the line in this family that has a distance from the center of the circle C(xc, yc) equal to the radius r, and from this, I determine the slope m.
$$ d = \frac{|ax_c + by_c + c|}{\sqrt{a^2 + b^2}} = r $$
The lines that satisfy this distance are tangent to the circle.
Example
Consider the point P(9, 0) and the following circle:
$$ x^2 + y^2 - 6x - 4y + 9 = 0 $$
Next, I calculate the coordinates of the center of the circle, knowing that a = -6 and b = -4:
$$ (x_0, y_0) = \left(-\frac{a}{2}, -\frac{b}{2}\right) $$
$$ (x_0, y_0) = \left(-\frac{-6}{2}, -\frac{-4}{2}\right) $$
$$ (x_0, y_0) = \left( 3, 2 \right) $$
The radius r is determined using this formula, knowing that a = -6, b = -4, and c = 9:
$$ r = \sqrt{\left(-\frac{a}{2}\right)^2 + \left(-\frac{b}{2}\right)^2 - c} $$
$$ r = \sqrt{\left(-\frac{-6}{2}\right)^2 + \left(-\frac{-2}{2}\right)^2 - 9} $$
$$ r = \sqrt{3^2 + 2^2 - 9} $$
$$ r = \sqrt{9 + 4 - 9} $$
$$ r = \sqrt{4} $$
$$ r = 2 $$
So, the center of the circle is at coordinates C(3, 2), and the radius is r = 2.
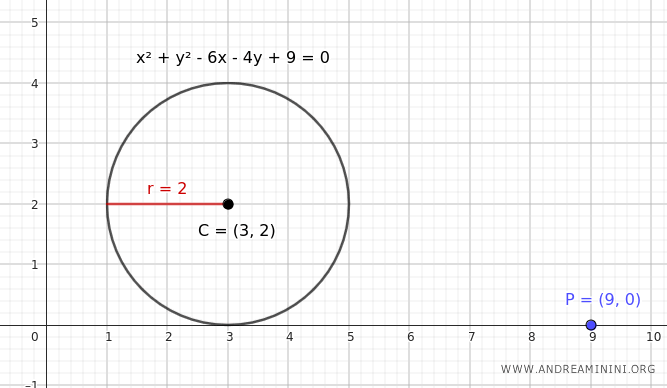
Now I write the equation of the family of lines passing through point P(x0, y0) = (9, 0):
$$ y - y_0 = m(x-x_0) $$
$$ y - 0 = m(x-9) $$
$$ y = mx - 9m $$
I write the equation of the family of lines in standard form, which is ax + by + c = 0. In this case, a = m, b = -1, c = -9m:
$$ mx - y - 9m = 0 $$
I find the lines that are at a distance from the center of the circle C(3, 2) equal to the radius r = 2, knowing that the coordinates of point C(3, 2) are xc = 3 and yc = 2, while the coefficients of the family of lines are a = m, b = -1, c = -9m.
$$ d = \frac{|ax_c + by_c + c|}{\sqrt{a^2 + b^2}} = r $$
$$ \frac{|m \cdot (3) - 1 \cdot (2) - 9m|}{\sqrt{m^2 + (-1)^2}} = 2 $$
$$ \frac{|3m - 2 - 9m|}{\sqrt{m^2 + 1}} = 2 $$
$$ \frac{|-6m - 2|}{\sqrt{m^2 + 1}} = 2 $$
$$ |-6m - 2| = 2 \cdot \sqrt{m^2 + 1} $$
I square both sides:
$$ (|-6m - 2|)^2 = (2 \cdot \sqrt{m^2 + 1})^2 $$
$$ (6m + 2)^2 = 4 \cdot (m^2 + 1) $$
$$ 36m^2 + 24m + 4 = 4m^2 + 4 $$
$$ 36m^2 + 24m + 4 - 4m^2 - 4 = 0 $$
$$ 32m^2 + 24m = 0 $$
At this point, I solve the equation to find m (the slope of the lines).
In this case, I factor out m instead of solving the quadratic equation:
$$ m \cdot (32m + 24) = 0 $$
The first solution is straightforward: m = 0.
$$ m_1 = 0 $$
The second solution is obtained by solving 32m + 24 = 0, which gives m = -3/4:
$$ m_2 = -\frac{24}{32} = -\frac{3}{4} $$
Finally, I go back to the equation of the family of lines and use the two slopes m1 = 0 and m2 = -3/4 that I just found.
$$ y = mx - 9m $$
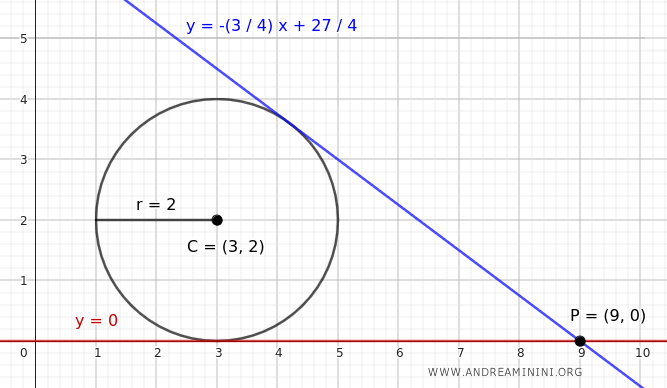
With m1 = 0, I get the equation of one tangent line: y = 0
$$ y = mx - 9m = 0 \cdot x - 9 \cdot 0 = 0 $$
With m2 = -3/4, I get the equation of another tangent line: y = -(3/4)x + 27/4
$$ y = mx - 9m = -\frac{3}{4} \cdot x - 9 \cdot (-\frac{3}{4}) = -\frac{3}{4}x + \frac{27}{4} $$
In this example, since P(9, 0) is a point outside the circle, there are two tangent lines to the circle passing through point P.
The Tangent Line Method Perpendicular to the Radius
This method is based on the principle that a tangent line at point P on a circle is always perpendicular to the radius at that point, according to the theorem of perpendicularity between a radius and a tangent.
Knowing that when two lines are perpendicular, the product of their slopes equals -1:
$$ m_r \cdot m_t = -1 $$
Thus, there is a relationship between the two slopes:
$$ m_t = - \frac{1}{m_r} $$
Once you have the equation of the line that includes the radius $ y = m_r x + q $, finding the equation of the tangent line becomes straightforward.
You simply apply the negative reciprocal of the slope to the equation that represents the family of lines passing through the point of tangency P(x0;y0).
$$ y-y_0 = m_t \cdot (x-x_0) $$
Note: This method only applies if point P is on the circumference. It does not apply if P is an external point.
Example
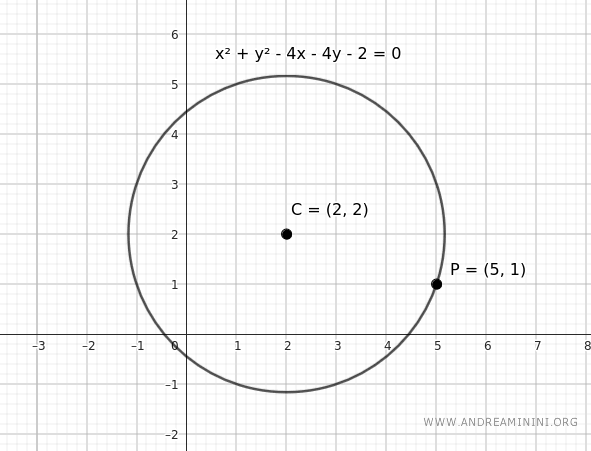
Consider a circle with the following equation:
$$ x^2+y^2-4x-4y-2=0 $$
We want to find the tangent line at point P(5,1) on the circle.
$$ P(5,1) $$
First, we calculate the center of the circle, knowing that in the equation of the circle, a=-4 and b=-4:
$$ (x_0, y_0) = \left(-\frac{a}{2}, -\frac{b}{2}\right) $$
$$ (x_0, y_0) = \left(-\frac{-4}{2}, -\frac{-4}{2}\right) $$
$$ (x_0, y_0) = \left( 2, 2 \right) $$
The center C of the circle is at coordinates (x,y)=(2,2)
$$ C(2,2) $$
Knowing the center of the circle C(2,2) and the point of tangency P(5,1), we find the equation of the line passing through the two points, which is the line containing the radius of the circle.
$$ \frac{y-y_c}{y_t-y_c}= \frac{x-x_c}{x_t-x_c} $$
The coordinates of the center C of the circle are (xc,yc)=(2,2) while those of the point of tangency P are (xt,yt)=(5,1)
$$ \frac{y-2}{1-2}= \frac{x-2}{5-2} $$
$$ \frac{y-2}{-1}= \frac{x-2}{3} $$
$$ y-2= - \frac{x-2}{3} $$
$$ y= - \frac{x-2}{3} +2 $$
$$ y= - \frac{x}{3} + \frac{2}{3} +2 $$
$$ y= - \frac{x}{3} + \frac{2+6}{3} $$
$$ y= - \frac{1}{3} \cdot x + \frac{8}{3} $$
Therefore, the slope of the line that includes the radius is mr=-1/3
$$ m_r = - \frac{1}{3} $$
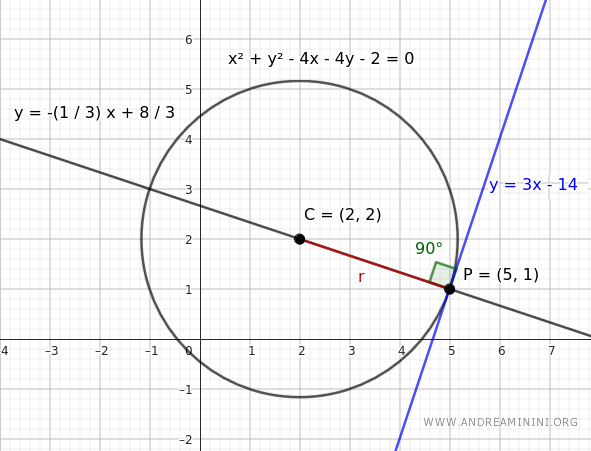
Knowing that the tangent line at point P is perpendicular to the radius, and that the product of the slopes of two perpendicular lines is mrmt=1, we deduce that the slope of the tangent line is mt=3.
$$ m_t = - \frac{1}{m_r} $$
$$ m_t = - \frac{1}{ - \frac{1}{3} } $$
$$ m_t = 3 $$
Now, we need to find the equation of the tangent line at point P(5,1).
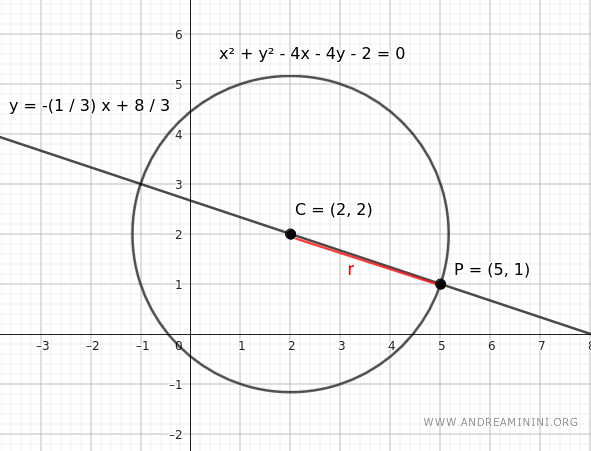
To find it, we use the equation of the family of lines passing through a point.
$$ y-y_0 = m \cdot (x-x_0) $$
We substitute the coordinates (x0,y0) with those of point P(5,1), i.e., x0=5 and y0=1.
$$ y-1 = m \cdot (x-5) $$
Since the slope we are interested in is mt=3, the equation of the tangent line at point P is:
$$ y-1 = 3 \cdot (x-5) $$
$$ y = 3x-15 + 1 $$
$$ y = 3x-14 $$
We have found the equation of the tangent line at point P.
The Tangent Line Formula Method
To find the equation of a tangent line at a point P(x0, y0) on a circle, you can use the tangent line formula:
$$ xx_0 + yy_0 + a \frac{x+x_0}{2} + b \frac{y+y_0}{2} + c = 0 $$
This formula directly provides the equation of the tangent line.
However, it can only be applied if P is a point on the circle; it does not work if P is outside the circle.
Example
Consider the same circle from the previous example:
$$ x^2 + y^2 - 4x - 4y - 2 = 0 $$
We need to find the equation of the tangent line at the point P(5,1) on the circle.
$$ P(5,1) $$
In this case, we use the tangent line formula:
$$ xx_0 + yy_0 + a \frac{x+x_0}{2} + b \frac{y+y_0}{2} + c = 0 $$
$$ xx_0 + yy_0 + \frac{a}{2}(x + x_0) + \frac{b}{2}(y + y_0) + c = 0 $$
For the circle \( x^2 + y^2 - 4x - 4y - 2 = 0 \), the coefficients are:
\( a = -4 \)
\( b = -4 \)
\( c = -2 \)
Substituting the coefficients \( a=-4 \), \( b=-4 \), and \( c=-2 \) into the tangent line formula:
$$ xx_0 + yy_0 + \frac{-4}{2}(x + x_0) + \frac{-4}{2}(y + y_0) - 2 = 0 $$
The coordinates of the tangent point P(5,1) are \( x_0 = 5 \) and \( y_0 = 1 \).
$$ x \cdot 5 + y \cdot 1 + \frac{-4}{2}(x + 5) + \frac{-4}{2}(y + 1) - 2 = 0 $$
$$ 5x + y - 2(x + 5) - 2(y + 1) - 2 = 0 $$
$$ 5x + y - 2x - 10 - 2y - 2 - 2 = 0 $$
$$ 3x - y - 14 = 0 $$
Therefore, the correct equation of the tangent line is:
$$ 3x - y - 14 = 0 $$
We have found the general equation of the tangent line.
Now, to find the slope of the line, we can solve for y:
$$ y = 3x - 14 $$
The slope of the tangent line is \( m = 3 \).

And so forth.
