Polygons Inscribed in Circles
A polygon that has all its vertices lying on the circumference of a circle is known as an inscribed polygon.
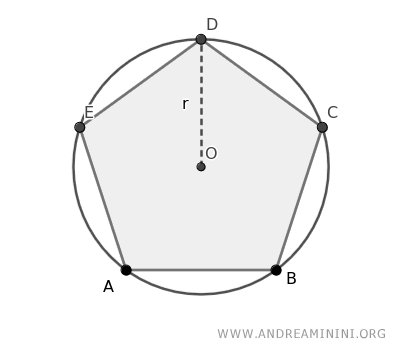
This relationship can also be described by saying that the circle circumscribes the polygon or the circle is circumscribed around the polygon. Essentially, it’s all the same concept.
Although the lengths of an inscribed polygon's sides may vary, every vertex of the polygon must touch the circle's circumference.
The circumcenter is the term for the center of this circumscribing circle.
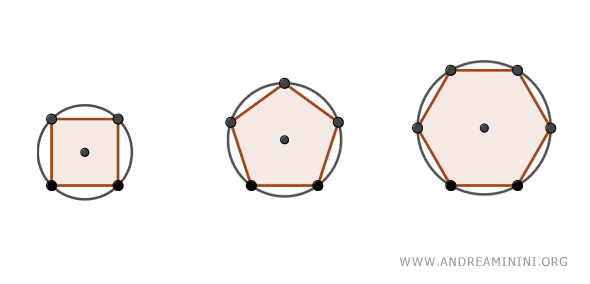
Not every polygon can be inscribed in a circle. Triangles, for example, can always fit within a circle, whereas only specific quadrilaterals have this property. In general, all regular polygons, such as pentagons, hexagons, etc., can be inscribed in a circle.
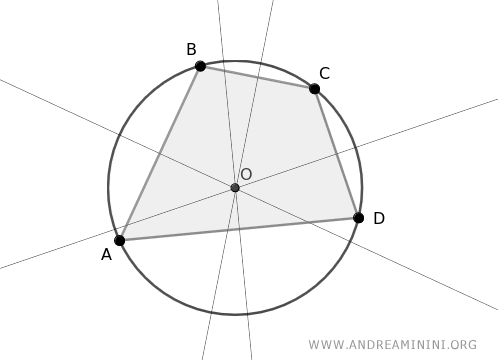
A quadrilateral inscribed in a circle will always have opposite angles that add up to 180° (α + β = 180°).
The Inscribed Polygon Theorem
A necessary and sufficient condition for a polygon to be inscribed in a circle is that the perpendicular bisectors of its sides intersect at a single point, known as the circumcenter.
If these perpendicular bisectors do not meet at one point, the polygon cannot be inscribed within a circle.
The converse is also true: if a polygon is inscribed in a circle, then the perpendicular bisectors of its sides will indeed meet at the center of the circle.
This unique point of intersection, the circumcenter, is a feature of all triangles, all regular polygons, and certain irregular polygons that can be inscribed in a circle.
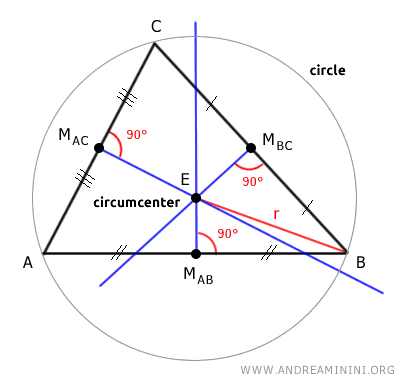
Putting It into Practice
Take the triangle as an example: its axes always converge at a common point known as the triangle's circumcenter.
By drawing a circle centered on the circumcenter (E) with a radius (r) that’s just right, the circle will encompass all the triangle's vertices.
The Proof
Consider a polygon where all the perpendicular bisectors of its sides converge at point O.
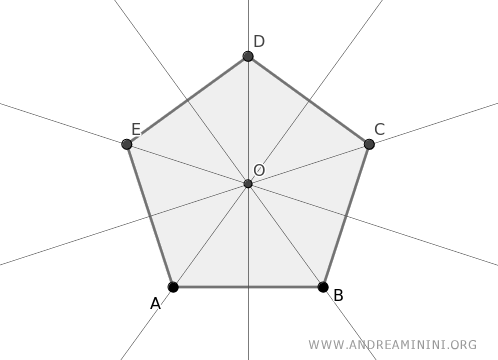
Here, the "axis" of a side refers to its perpendicular bisector, which is a line that crosses the midpoint of the side at a right angle (90°).
Our goal is to demonstrate that such a polygon can be inscribed in a circle.
By definition, an axis is the geometric place of points equidistant from the endpoints of a segment.
Hence, any point on an axis is equidistant from both endpoints of a side of the polygon.
For instance, point P on the axis of side AB is equidistant from endpoints A and B.
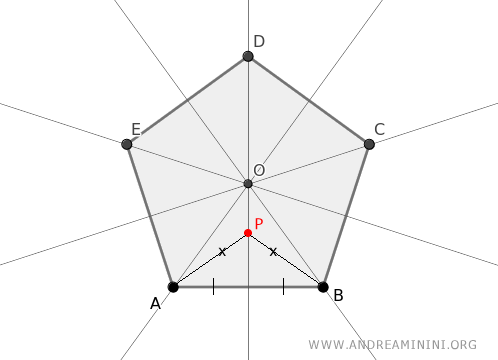
This implies that the intersection point O, where the axes meet, is equidistant from all vertices of the polygon.
In simpler terms, the distance d from point O to any vertex of the polygon is consistent.
$$ d = \overline{OA} = \overline{OB} = \overline{OC} = \overline{OD} = \overline{OE} $$
Thus, a circle with center O (circumcenter) and radius d can be drawn, passing through every vertex of the polygon and thereby circumscribing the polygon.
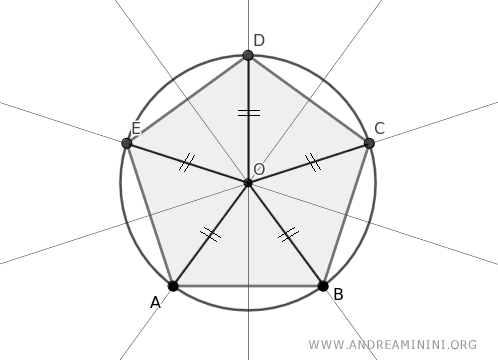
This proves that the polygon is inscribed within a circle.
And so forth.
