Central Axis of a Pencil of Circles
The central axis of a pencil of circles is a line that represents the geometric locus of the centers of all the circles in the pencil.

In other words, it is the line along which the centers of all the circles generated from a particular family of circles lie.
A pencil of circles is the set of all circles that can be described by the general equation:
$$ C_1 + \lambda C_2 = 0 $$
Where \(C_1\) and \(C_2\) are two generating circles of the pencil, and \(\lambda\) is a real parameter.
The central axis of this pencil is the line that passes through the centers of the two circles \(C_1\) and \(C_2\) and is perpendicular to the radical axis.
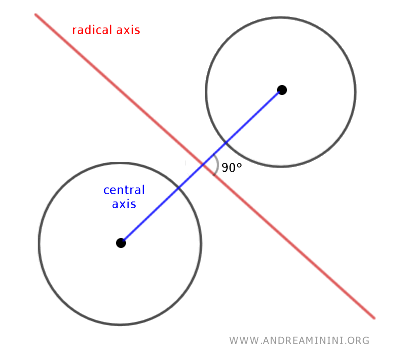
Every circle generated in the pencil will have its center on the central axis.
Thus, it can be thought of as a sort of "path of centers" for the circles in the pencil.

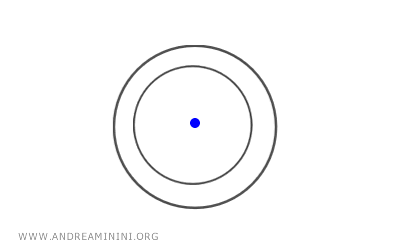
If the generating circles \(C_1\) and \(C_2\) are concentric (having the same center), the central axis of the pencil reduces to a single point, the common center of the circles.
Note: The concept of the central axis can be extended to higher dimensions, such as in the analysis of pencils of spheres in three-dimensional geometry. In this case, the central axis would become a plane along which the centers of all the spheres in the pencil lie.
A Practical Example
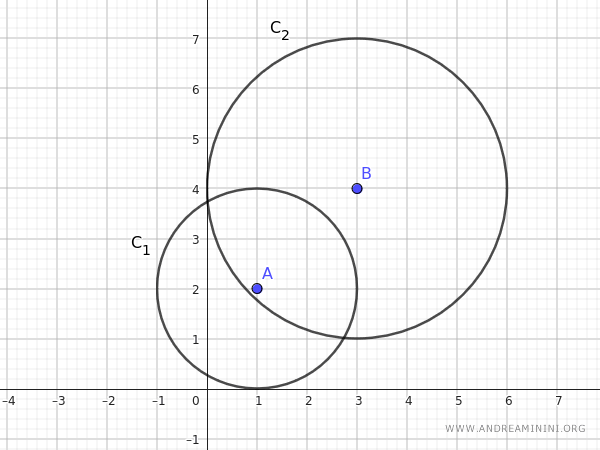
Consider two generating circles with the following equations:
$$ C_1: (x - 1)^2 + (y - 2)^2 - 4 = 0 $$
$$ C_2: (x - 3)^2 + (y - 4)^2 - 9 = 0 $$
The centers of the circles \(C_1\) and \(C_2\) are \( A= (1, 2) \) and \( B= (3, 4) \) respectively.
The central axis of the pencil is the line that passes through these two points. The equation of the line can be found using the formula for a line passing through two points:
$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$
Substituting the coordinates of the centers of the circles:
$$ \frac{y - 2}{4 - 2} = \frac{x - 1}{3 - 1} $$
$$ \frac{y - 2}{2} = \frac{x - 1}{2} $$
Multiplying both sides by 2, we get:
$$ y - 2 = x - 1 \implies y = x + 1 $$
Therefore, the central axis of the pencil of these circles is the line \( y = x + 1 \).
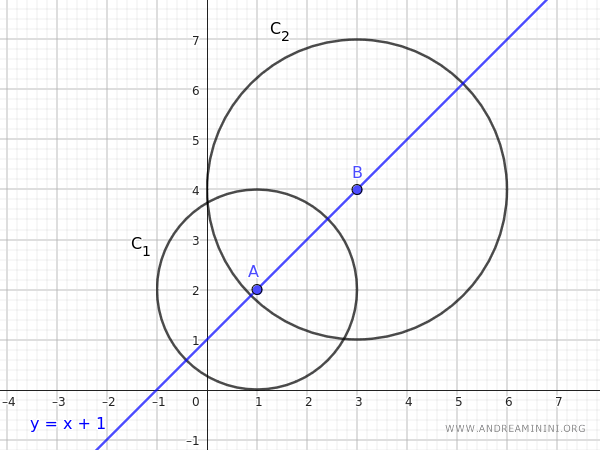
The central axis of the pencil of circles is the line that contains the centers of the circles in the pencil.
Let’s construct the pencil of lines from the two circles.
$$ C_1 + \lambda C_2 = 0 $$
$$ [ (x - 1)^2 + (y - 2)^2 - 4 ] + \lambda \cdot [ (x - 3)^2 + (y - 4)^2 - 9 ] = 0 $$
We generate a circle from the pencil using the value \(\lambda = 2\)
$$ [ (x - 1)^2 + (y - 2)^2 - 4 ] + 2 \cdot [ (x - 3)^2 + (y - 4)^2 - 9 ] = 0 $$
$$ [ x^2-2x+1 + y^2-4y+4 - 4 ] + 2 \cdot [ x^2 - 6x+ 9 + y^2-8y +16 - 9 ] = 0 $$
$$ x^2-2x+1 + y^2-4y + 2x^2 - 12x + 2y^2 -16y+32= 0 $$
$$ 3x^2 + 3y^2 -14x -20y+33= 0 $$
Dividing everything by three:
$$ x^2 + y^2 - \frac{14}{3}x - \frac{20}{3}y + 11 = 0 $$
This circle belongs to the pencil and has its center at
$$ \left( -\frac{a}{2} , -\frac{b}{2} \right) $$
$$ \left( -\frac{-\frac{14}{3}}{2} , -\frac{-\frac{20}{3}}{2} \right) $$
$$ \left( \frac{14}{6} , \frac{20}{6} \right) $$
$$ \left( \frac{7}{3} , \frac{10}{3} \right) $$
The center \((7/3, 10/3)\) of the generated circle lies on the central axis of the pencil of circles.
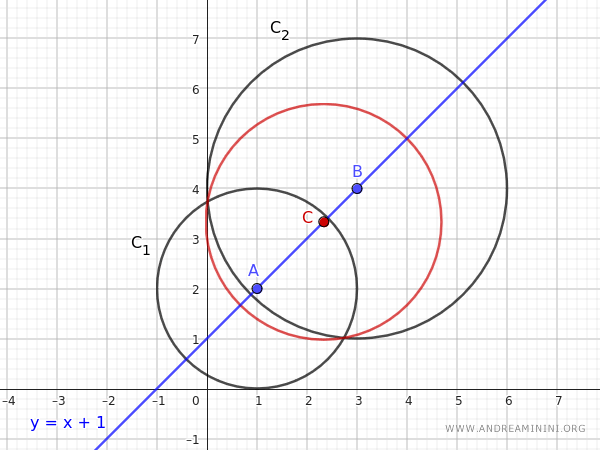
The same holds true for all other circles generated by the pencil of circles.
And so on.
