The Tangent Theorem for a Circle from an External Point

Consider a circle with two tangent lines passing through a point P outside the circle. The segments connecting point P to the points of tangency, T₁ and T₂, are congruent, $ \overline{PT_1} \cong \overline{PT_2} $ (i.e., they are of equal length).

 

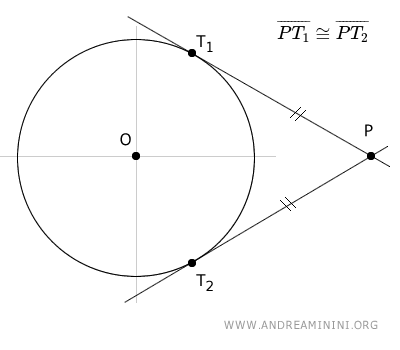
Additionally, there are three important properties to note:

• The segment OP, connecting the center O of the circle with the external point P, is the axis of the chord between the points of tangency T₁ and T₂, and acts as the symmetry axis for the segments PT₁ and PT₂.
  
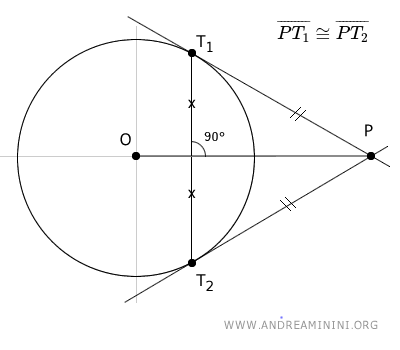
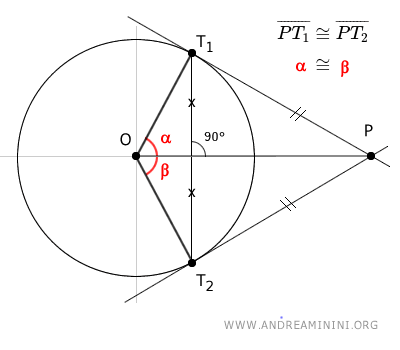
• The segment OP bisects the (red) angle formed by the radii of the circle that connect the center O to the points of tangency T₁ and T₂.
  
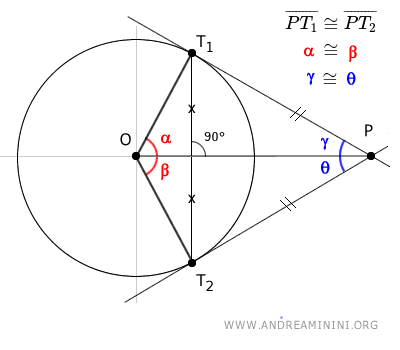
• The segment OP also bisects the (blue) angle formed by the two tangent lines PT₁ and PT₂ at point P.
  

Proof

Consider a circle with radius OT₁ and two tangent lines PT₁ and PT₂ passing through the external point P.

Draw the segment connecting the center of the circle O to the external point P.

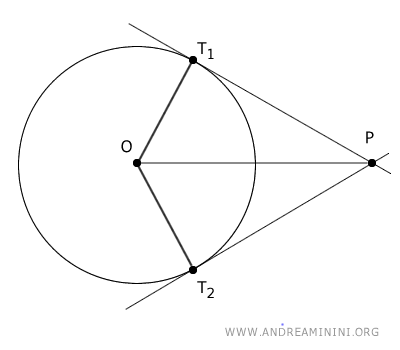
The points of tangency on the circle are T₁ and T₂.

The segments OT₁ and OT₂ are congruent because they are both radii of the circle.

$$ \overline{OT_1} \cong \overline{OT_2} $$

Knowing that the radii of the circle are always perpendicular to the tangent lines, we deduce that the radii OT₁ and OT₂ form a 90° angle with the segments PT₁ and PT₂, respectively.

$$ \overline{OT_1} \perp \overline{PT_1} $$

$$ \overline{OT_2} \perp \overline{PT_2} $$

Therefore, the triangles OPT1 and OPT2 are both right triangles.

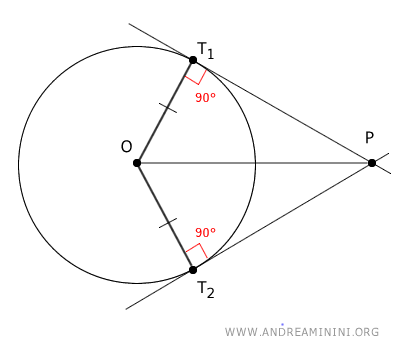
The two right triangles OPT₁ and OPT₂ are congruent by the right triangle congruence theorem because they have one congruent leg OT₁ = OT₂ and a common hypotenuse OP.

$$ OPT_1 \cong OPT_2 $$

Since the two triangles are congruent, all their sides and angles are congruent in the same order.

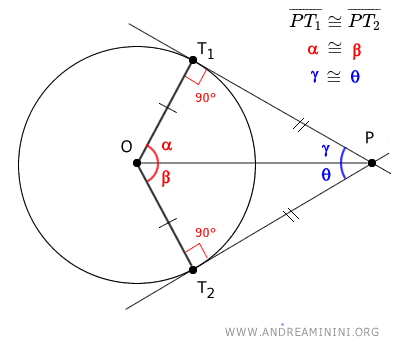
This shows that the segments PT₁ and PT₂ are congruent.

$$ \overline{PT_1} \cong \overline{PT_2} $$

Additionally, angles α = β and γ = θ are congruent.

$$ \alpha \cong \beta $$ $$ \gamma \cong \theta $$

Therefore, the segment OP bisects both the central angle O formed by the radii and the angle between the tangent lines at point P.

Finally, draw the chord T₁T₂ between the two points of tangency.

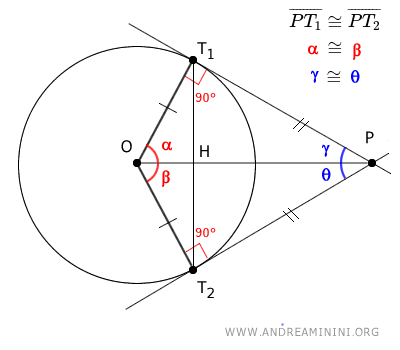
The triangle OT₁T₂ is an isosceles triangle because the two sides OT₁ ≅ OT₂ are congruent, being radii of the circle.

The segment OH is a bisector of the triangle because we already know that angles α ≅ β are congruent.

Knowing that in an isosceles triangle, the bisector coincides with the height, the axis, and the median, we deduce that:

• The segment OH is perpendicular to the chord T₁T₂ because OH is the height of the triangle.
• Point H is the midpoint of the chord T₁T₂ because OH is also the median.

Therefore, segment OH is an axis of the triangle OT₁T₂.

Since OH is part of segment OP, this proves that segment OP is the axis of the chord T₁T₂ between the two points of tangency.

And there you have it.