Principles of Congruence in Circles
Within a circle, congruence can be observed between:
- two central angles
- two arcs
- two chords
- two circular segments
- two circular sectors
When any of these elements are congruent, the corresponding figures are also congruent.
Put simply, these geometric shapes within a circle are interconnected; the congruence of one element, such as central angles or chords, suggests congruence across the others.
Note: It's important to recognize that congruence among elements within the same circle, like central angles, arcs, chords, circular sectors, and circular segments, does not imply that two distinct circles are congruent. To determine circle congruence, comparing their radii is the only method.
This occurs because each shape inherently defines the others. For example, an arc is intrinsically linked to its central angle, chords, circular sector, and circular segment.
Take the chord AB in a circle, for instance.
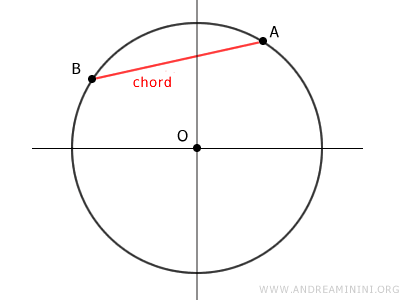
This chord AB determines an arc AB, which in turn correlates with a central angle α, a circular sector, and a circular segment.
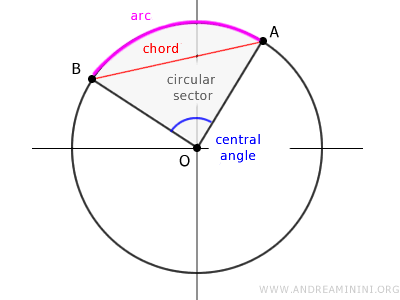
These relationships are one-to-one, meaning that each arc exactly corresponds to a specific central angle and vice versa.
Consequently, the congruence between two chords in a circle also ensures the congruence of their respective arcs, circular sectors, chords, and central angles.
This principle extends to all other figures as well.
