Circle
A circle is a two-dimensional geometric shape comprised of all the points on its circumference and those within.
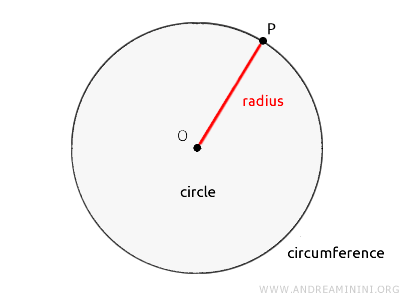
Alternatively, you can think of a circle as the set of all points in a plane at a distance from a central point, O, that is equal to or less than its radius (r).
The radius is the segment connecting the circle's center (O) to any point along its edge.
Circles have fascinated humans for millennia, drawing the attention of ancient civilizations like the Egyptians, Babylonians, and Greeks, who studied their properties and used them in everything from architecture to astronomy.
Circle Basics
The circumference acts as the circle's perimeter.
The formula for the circumference, C, involves multiplying the diameter (d) by the mathematical constant π (pi).
$$ C = \pi \cdot d $$
Since the diameter is simply twice the radius (d=2r), the formula can also be expressed as C=2πr, where r represents the circle's radius.
$$ C = 2 \pi \cdot r $$
The constant π (pi) symbolizes the ratio of a circle’s circumference to its diameter, a value roughly equal to 3.14. This constant remains the same regardless of the circle's size because the ratio of the circumference to the diameter is always the same.
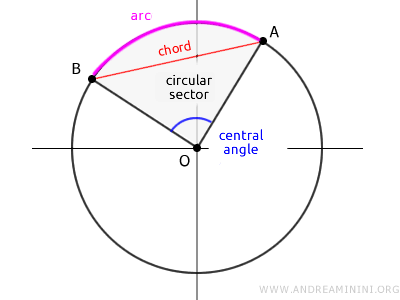
An arc is essentially a slice of the circle’s edge.
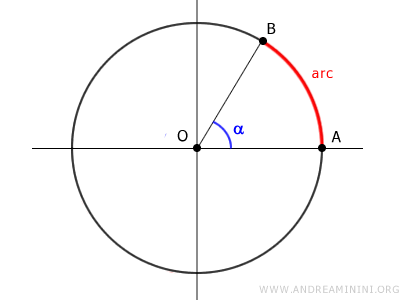
The length of an arc (L) correlates directly with the central angle (α) it spans.
$$ L:C = \alpha : 360° $$
This means the length of an arc compared to the full circle's circumference is the same as the ratio of its central angle to 360 degrees.
To find the area of a circle, multiply π (approximately 3.14) by the square of the radius (r).
$$ A = \pi r^2 $$
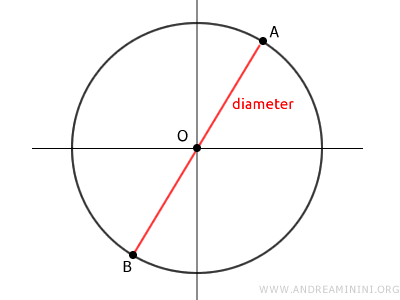
The diameter is a straight line that runs through the circle's center and touches two points on its boundary, exactly double the radius in length.
A chord is a line segment whose endpoints lie on the circle's circumference, but unlike diameters, chords do not have to pass through the center.
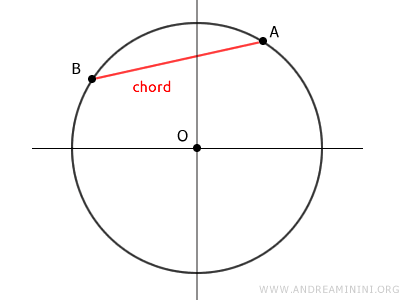
Any chord splits the circle into two regions, each known as a circular segment or a segment of a circle based on one boundary.
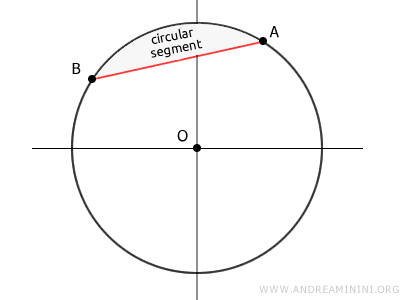
If a circular segment is smaller than a semicircle, its area equals the area of the corresponding circular sector minus the area of triangle OAB if the sector.
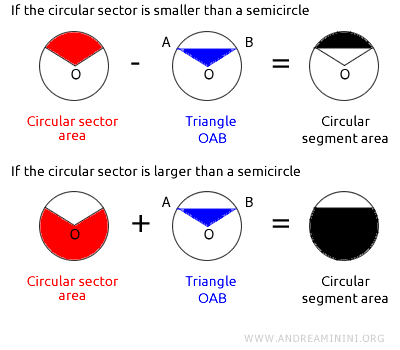
If, however, the circular segment is larger than a semicircle, its area is the sum of the circular sector's area and the area of triangle OAB.
By semicircle, we mean half of a circle.
A circular segment based on two boundaries, known as a circular segment with two bases, sits between two parallel chords.
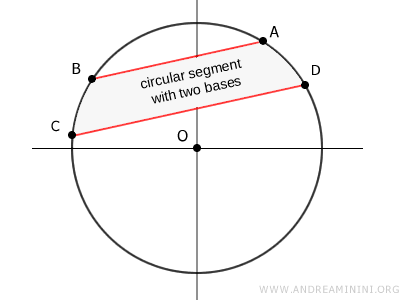
To calculate its area, subtract the combined areas of the two one-based segments created by chords AB and CD from the circle's total area (A).
A sector (or circular sector) is the wedge-shaped part of the circle carved out by two radii and the arc between them.
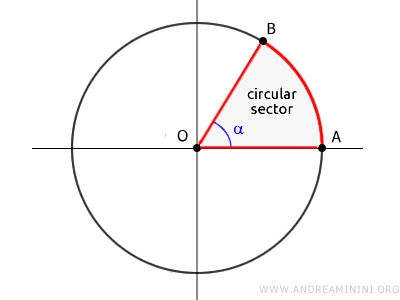
The area of the sector is proportional to the size of its central angle (α).
$$ A_s : A = \alpha : 360° $$
This formula shows that the sector's area as a fraction of the circle's total area is equivalent to the central angle's fraction of a full circle (360 degrees).
The annular ring refers to the area enclosed by two concentric circles with the same center but different radii.
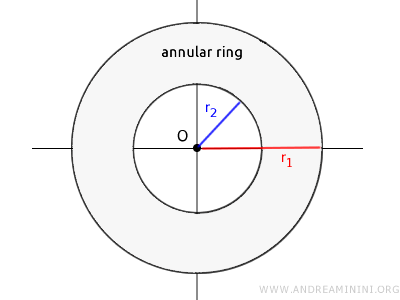
Its area is the difference between the areas of the larger and smaller circles.
$$ A_c = \pi \cdot r_1^2 - \pi \cdot r_2^2 $$
Circle Formulas at a Glance
Essential formulas for determining circle dimensions include:
- Circumference
The formula for the circumference (C) is twice the radius (r) times π (3.14) $$ C=2r \cdot \pi $$ Given that the diameter is twice the radius, the equivalent formula is $$ C = d \cdot \pi $$ - Area
The area of a circle is the square of the radius (r) times π (3.14) $$ A = r^2 \cdot \pi $$ - Arc Length
The arc's length (L) is proportional to the central angle (α) it spans $$ L:C = α:360° $$ Thus, the arc's length is determined by the formula $$ L = \frac{ \alpha \cdot C }{360} $$ - Area of a Sector
The area of a sector As is proportional to the central angle (α) it covers $$ A_s : A = α:360° $$ Consequently, the sector's area is found with the formula $$ A_s = \frac{ \alpha \cdot A } {360} $$ - Area of an Annular Ring
The annular ring's area Ac is found by subtracting the smaller circle's area from the larger one's $$ A_c = \pi \cdot r_1^2 - \pi \cdot r_2^2 = \pi \cdot (r_1^2 - r_2^2) $$
Insights into Circles
Noteworthy observations about circles include:
- Circles are convex shapes, meaning any segment connecting two points within a circle lies entirely within it.
Proof. A convex shape is defined such that any line segment connecting two points inside the shape remains entirely within it. Consider any two points A and B inside the circle and the segment AB connecting them. There are two scenarios:
1] If A and B are on the same diameter, the segment AB is at most as long as the diameter, ensuring it lies entirely within the circle.
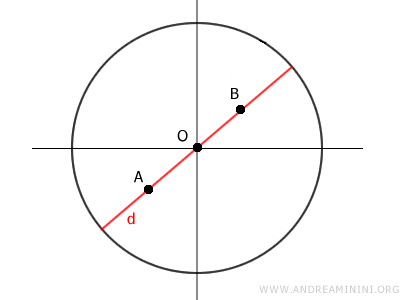
2] If A and B are not on the same diameter, a triangle OAB is formed with O being the circle's center. Taking any point C on AB, one can show that OC is always shorter than OA or OB, proving the segment's entirety lies within the circle.
This demonstrates that any segment within the circle remains inside, proving the circle's convex nature. - Principles of Congruence in Circles
Within a circle, if two chords, arcs, sectors, segments, or central angles are congruent, then all corresponding figures are also congruent, reflecting a one-to-one correspondence within the circle's geometry.
And so forth
