Tangent, Secant, or External Line to a Circle

A line is tangent to a circle if they intersect at exactly one point, external if they don't intersect at all, and secant if they intersect at two points.

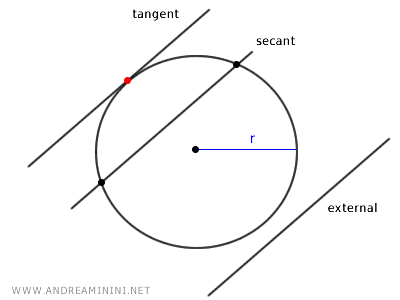
How to Determine if a Line is Tangent, Secant, or External to a Circle

To determine if a line is tangent, external, or secant in analytic geometry, you need to know the radius \( r \) and the center of the circle \( C(x₀, y₀) \), as well as the equation of the line \( y = mx + q \).

When a circle is tangent to a line, the distance between them is equal to the radius.

The formula for the distance from a point \((x_0, y_0)\) to the line \( y = mx + q \) is:

$$ d = \frac{|mx_0 - y_0 + q|}{\sqrt{m^2 + 1}} $$

Comparing the radius to the distance, three scenarios can occur:

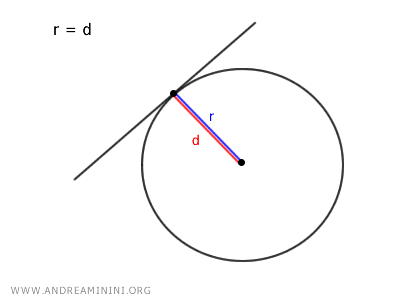
• If r = d, the radius is equal to the distance, so the line is tangent to the circle.
  
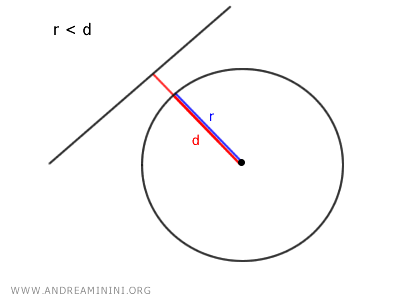
• If r < d, the radius is less than the distance, so the line is external to the circle.
  
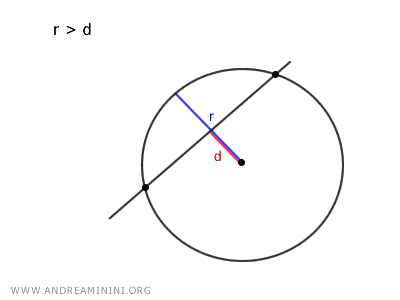
• If r > d, the radius is greater than the distance, so the line is secant and intersects the circle at two distinct points.
  

A Practical Example

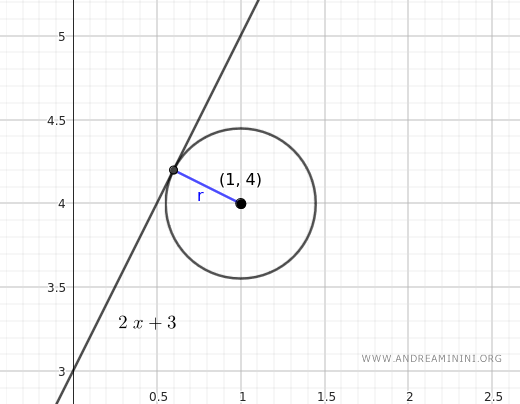
In this example, consider the equation of the line:

$$ y = 2x + 3 $$

The circle has its center at point \( C(1, 4) \) and a radius of:

$$ r = \frac{1}{\sqrt{5}} $$

To determine if the line is tangent, secant, or external to the circle, we calculate the Euclidean distance between the line and the center of the circle.

The formula for the distance \( d \) from a point \((x_0, y_0)\) to the line \( y = mx + q \) is:

$$ d = \frac{|mx_0 - y_0 + q|}{\sqrt{m^2 + 1}} $$

In this case, the equation of the line is \( y = 2x + 3 \), so \( m = 2 \) and \( q = 3 \).

$$ d = \frac{|2x_0 - y_0 + 3|}{\sqrt{2^2 + 1}} $$

$$ d = \frac{|2x_0 - y_0 + 3|}{\sqrt{4 + 1}} $$

The center of the circle is \( C(1, 4) \), so \( x_0 = 1 \) and \( y_0 = 4 \).

$$ d = \frac{|2 \cdot 1 - 4 + 3|}{\sqrt{4 + 1}} $$

$$ d = \frac{|2 - 1|}{\sqrt{5}} $$

$$ d = \frac{|1|}{\sqrt{5}} $$

$$ d = \frac{1}{\sqrt{5}} $$

The radius of the circle and the distance are equal, so the line is tangent to the circle.

$$ r = d = \frac{1}{\sqrt{5}} $$

Here is the graphical representation of the problem:

And so on.