Semicircle

A semicircle is a plane figure defined by a diameter and the arc of the circle it belongs to.

In simple terms, as its name implies, a semicircle is exactly half of a circle, divided along its diameter.

The radius of a semicircle is identical to that of the original circle from which it’s derived.

Its diameter is also the same as that of the original circle and forms the base of the semicircle.

$$ d = 2r $$

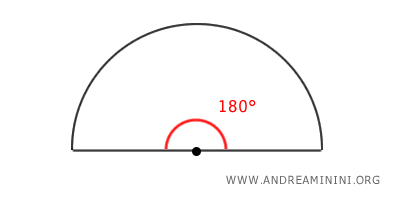
The central angle of a semicircle always measures 180°, as it represents half of a full rotation (360°) around the circumference of the circle.

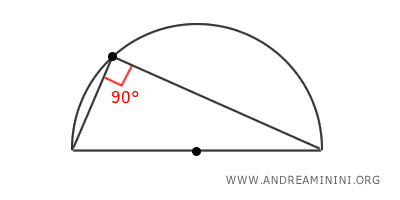
Meanwhile, any angle inscribed in the semicircumference is always a right angle of 90°.

The area of a semicircle is half the area of the corresponding full circle. The formula for calculating the area of a semicircle is:

$$ A = \frac{\pi \cdot r^2}{2} $$

where r is the radius of the semicircle.

The perimeter of a semicircle is found by adding the length of its diameter (d) to the length of its arc, which is half the circumference of the full circle, equal to πr. The formula is:

$$ P = 2r + \pi r $$

And so on.