Area of a Regular Polygon

The area of a regular polygon is calculated by multiplying the semiperimeter (p) by the apothem (a): $$ A = p \cdot a $$ where the apothem is the distance from the center to any side, and the semiperimeter is half the perimeter, so 2p = P, thus p = P/2.

Explanation

The concept involves dividing a regular polygon into several congruent triangles, each with one vertex at the center of the polygon and the base being one side of the polygon.

For instance, a hexagon can be divided into 6 congruent triangles.

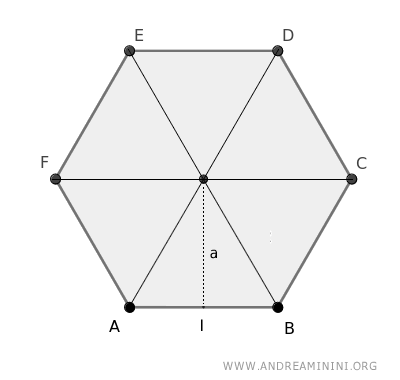
The area of each triangle is calculated using the basic formula: base (l) times height (h) divided by two.

$$ \frac{l \cdot h}{2} $$

In polygons, the height of the triangles coincides with the apothem (a), which is the distance from the center to any side of the polygon.

Therefore, the area formula for a triangle can be rewritten as:

$$ \frac{l \cdot a}{2} $$

Once the area of one triangle is found, multiply it by the number of triangles (the number of sides of the polygon) to find the total area of the polygon.

$$ A = n \cdot \frac{l \cdot a}{2} $$

For example, to find the area of a hexagon, calculate the area of one triangle and multiply it by 6. $$ A = 6 \cdot \frac{l \cdot a}{2} $$

Knowing that the perimeter of a regular polygon is the product of the number of sides (n) and the length of a single side (l), written as P=n·l, we can rewrite the previous formula in a more compact form:

$$ A = \frac{P \cdot a}{2} $$

The capital letter P represents the perimeter of the polygon.

Since in geometry, the lowercase "p" indicates the semiperimeter, which is half the perimeter (P), or p=P/2, we can further simplify the area formula as follows:

$$ A = p \cdot a $$

This makes the formula much easier to remember.

In conclusion, this demonstrates that the area of a regular polygon is equal to the product of the semiperimeter (p) and the apothem (a).

A Practical Example

Let's consider a regular hexagon where each side is l=6 and the apothem is a=5.2.

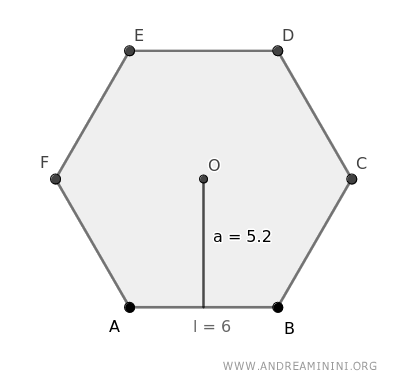
First, calculate the perimeter (P), knowing that the hexagon has six sides.

$$ P = 6 \cdot 6 = 36 $$

Then, divide it in half to get the semiperimeter (p)

$$ p = \frac{P}{2} = \frac{36}{2} = 18 $$

Finally, multiply the semiperimeter (p=18) by the apothem (a=5.2) to find the area of the hexagon (A)

$$ A = p \cdot a = 18 \cdot 5,2 = 93,6 $$

The area of the hexagon is 93.6

Note: Alternatively, you could calculate the area of a single triangle using the formula base (l) times height (h) divided by two, knowing that the side is l=6 and the height coincides with the apothem h=a=5.2 $$ A_t = \frac{l \cdot h}{2} = \frac{6 \cdot 5,2}{2} = \frac{31,2}{2} = 15,6 $$ Once you get the area of one triangle (A_t=15.6), just multiply it by the number of triangles the hexagon is divided into. In this case, the number of triangles is n=6 $$ A = A_t \cdot n = 15,6 \cdot 6 = 93,6 $$ The final result is the area of the hexagon.

This formula works for all regular polygons, not just hexagons.

Whether it’s a pentagon, octagon, or decagon, the formula remains the same.

Example 2

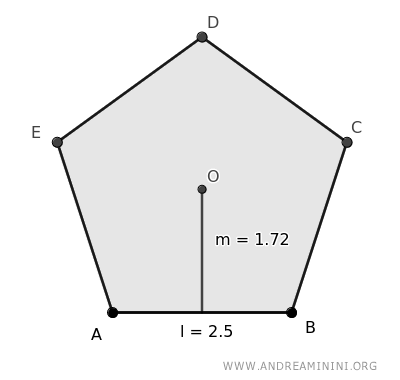
Consider a pentagon with sides of length l=2.5 and an apothem a=1.72

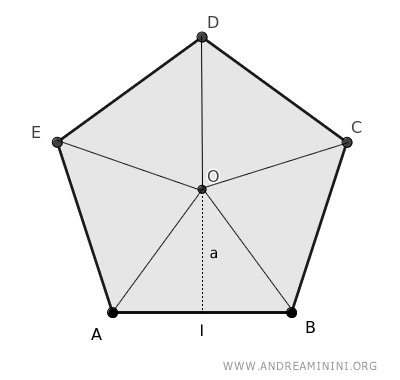
Note: In plane geometry, a pentagon can be divided into five triangles.

Calculate the perimeter (P) of the pentagon, knowing it has n=5 sides and each side is l=2.5

$$ P = n \cdot l = 5 \cdot 2,5 = 12,5 $$

Then calculate the semiperimeter (p), knowing that 2p=P=12.5

$$ p = \frac{P}{2} = \frac{12,5}{2} = 6,25 $$

Finally, find the area of the pentagon (A) by multiplying the semiperimeter p=6.25 by the apothem a=1.72

$$ A = p \cdot a = 6,25 \cdot 1,72 = 10,75 $$

Thus, the area of the pentagon is A=10.75

Observations and Notes

Here are some additional observations and notes:

• Inverse Formulas
  From the direct formula $$ A=p \cdot a $$, we get the inverse formulas to calculate the semiperimeter given the area and apothem, or the apothem given the area and semiperimeter: $$ p = \frac{A}{a} $$ $$ a = \frac{A}{p} $$ Knowing that the perimeter is twice the semiperimeter P=2p: $$ P = 2p = \frac{2A}{a} $$
• The Apothem is Always Perpendicular to the Side of the Polygon
  In a regular polygon, the apothem is also the radius of the inscribed circle. This can be useful when the radius of the inscribed circle is known, but the apothem is not.
• Polygons with a Large Number of Sides
  As the number of sides of a regular polygon increases, the polygon tends to become a circle. In this case, the apothem tends to become the radius of the circle.
• Relationship Between Apothem, Radius, and Angles
  The apothem, the radius, and the internal angles of a regular polygon are interconnected. For example, in a regular hexagon, the central angle is 60° (360°/6). Using trigonometric functions, the apothem can be found given the radius, and vice versa.
• Equivalence Between a Regular Polygon and a Triangle
  The area of a regular polygon is equal to that of a triangle with a base equal to the perimeter of the regular polygon and a height equal to the apothem of the regular polygon.
  

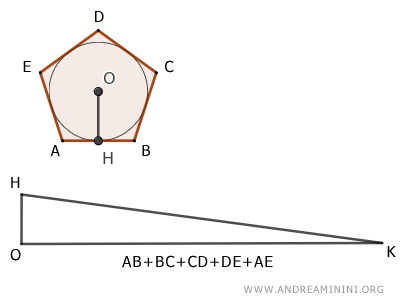
And so on