Calculating the Area of an Irregular Polygon
Finding the area of an irregular polygon or any plane figure is more complex than calculating the area of regular polygons. However, there are various methods to achieve this, depending on the available information and the specific characteristics of the polygon. Here are some common techniques:
Decomposition into Regular Polygons
A plane figure can be divided into simpler shapes like triangles, rectangles, trapezoids, etc.
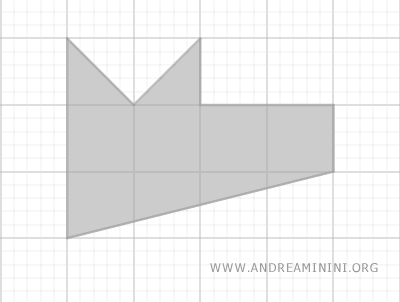
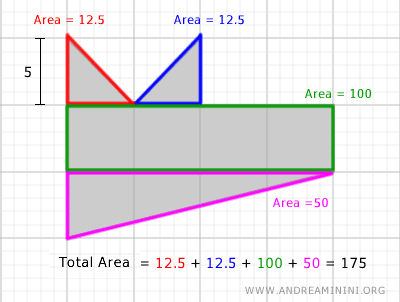
The area of the irregular polygon is determined by summing the areas of these simpler shapes.
When a figure or part of a figure cannot be divided into regular polygons, an estimate can be made.
For instance, consider this curvilinear figure:
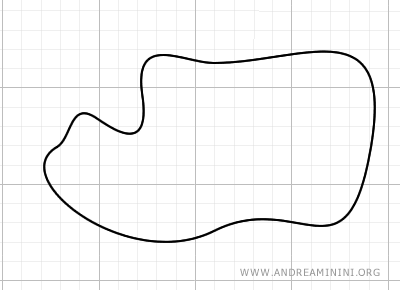
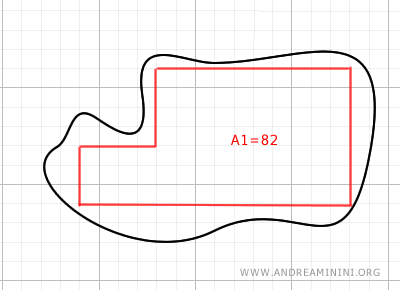
To estimate the area, draw a polygonal line inside the figure, minimizing the empty spaces.
Then, divide the area into regular polygons, calculate the area of each, and sum them up.
This gives us the area A1=82 of the inscribed polygonal line.
Next, draw a polygonal line around the outside of the curvilinear figure, again minimizing empty spaces.
Then, divide this outer polygonal line into regular polygons, calculate the area of each, and sum them up.
This gives us the area A2 of the circumscribed polygonal line.
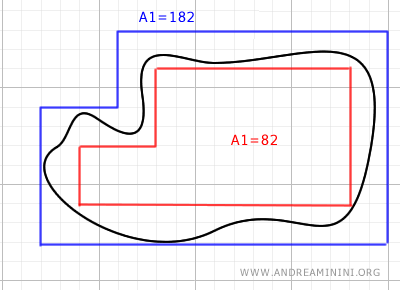
At this point, we can state that the area of the irregular figure is between the area of the inscribed polygonal line A1=82 and the area of the circumscribed polygonal line A2=182.
$$ A_1 < A < A_2 $$
$$ 82 < A < 182 $$
Finally, we calculate the average of these two approximate values.
$$ A = \frac{A_1 + A_2}{2} $$
$$ A = \frac{82 + 182}{2} $$
$$ A = \frac{264}{2} $$
$$ A = 132 $$
The area of the plane figure is approximately 132 square units.
Using this method, we can get an approximate estimate of the area of any plane figure.
Note: This is, of course, an estimate. The accuracy depends on the granularity of the division. The smaller the regular polygons used for approximation, the more accurate the estimate will be.
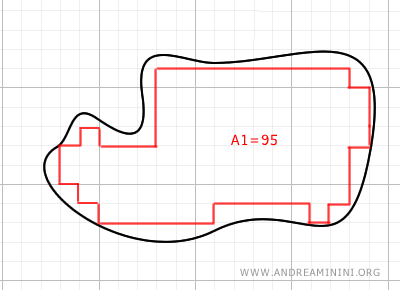
This approximate calculation method is developed in mathematical analysis and is the basis of Riemann definite integrals.
The Shoelace Formula (or Gauss's Area Formula)
This formula is useful if you know the coordinates of the vertices of the irregular polygon. Assuming the polygon has vertices (x1,y1), (x2,y2), ..., (xn,yn), and that (xn+1,yn+1)=(x1,y1), the area A of the polygon is given by the following summation:
$$ A = \frac{1}{2} \cdot \left| \sum_{i=1}^{n} ( x_i y_{i+1} - x_{i+1} y_i ) \right| $$
For example, consider this irregular polygon:
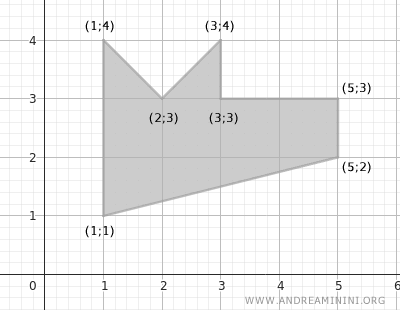
The coordinates of the polygon are:
$$ (x_1;y_1) = (1;1) \\ (x_2;y_2) = (1;4) \\ (x_3;y_3) = (2;3) \\ (x_4;y_4) = (3;4) \\ (x_5;y_5) = (3;3) \\ (x_6;y_6) = (5;3) \\ (x_7;y_7) = (5;2) $$
Since the polygonal line must be closed, we add another coordinate that coincides with the initial one:
$$ (x_8;y_8) = (1;1) $$
Now, we apply the formula to calculate the summation:
$$ A = \frac{1}{2} \cdot \left| \sum_{i=1}^{7} ( x_i y_{i+1} - x_{i+1} y_i ) \right| $$
$$ A = \frac{1}{2} \cdot \left| (x_1 y_2 - x_2 y_1) + (x_2 y_3 - x_3 y_2) + (x_3 y_4 - x_4 y_3) + \\ \ \ \ \ + (x_4 y_5 - x_5 y_4) + (x_5 y_6 - x_6 y_5) + (x_6 y_7 - x_7 y_6) + (x_7 y_8 - x_8 y_7) \right| $$
Substitute the x-coordinates: x1=1, x2=1, x3=2, x4=3, x5=3, x6=5, x7=5, x8=1 and the y-coordinates: y1=1, y2=4, y3=3, y4=4, y5=3, y6=3, y7=2, y8=1
$$ A = \frac{1}{2} \cdot \left| (1 \cdot 4 - 1 \cdot 1) + (1 \cdot 3 - 2 \cdot 4) + (2 \cdot 4 - 3 \cdot 3) + \\ \ \ \ \ + (3 \cdot 3 - 3 \cdot 4) + (3 \cdot 3 - 5 \cdot 3) + (5 \cdot 2 - 5 \cdot 3) + (5 \cdot 1 - 1 \cdot 2) \right| $$
Perform the calculations:
$$ A = \frac{1}{2} \cdot \left| (4 - 1) + (3 - 8) + (8 - 9) + (9 - 12) + (9 - 15) + (10 - 15) + (5 - 2) \right| $$
$$ A = \frac{1}{2} \cdot \left| 3 - 5 - 1 - 3 - 6 - 5 + 3 \right| $$
$$ A = \frac{1}{2} \cdot |-14| $$
$$ A = \frac{1}{2} \cdot 14 $$
$$ A = 7 $$
Since each square is composed of 5x5=25 unit squares,
The area of the irregular polygon is 25×7, which is 175 unit squares.
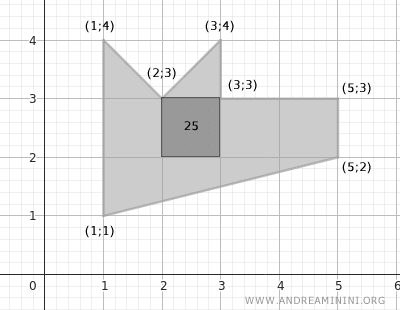
This is the same result obtained previously.
And so on.
