Area of a Polygon Circumscribed Around a Circle

The area of a polygon circumscribed around a circle is calculated by multiplying the polygon's semiperimeter (p) by the radius (r) of the circle. $$ A = p \cdot r $$ Here, the semiperimeter (p) is half of the polygon's perimeter (P), so p = P/2.

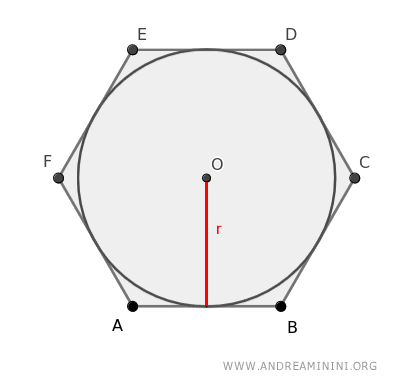
In simpler terms, the area of a polygon circumscribed around a circle can be found by multiplying the perimeter by the radius of the inscribed circle and dividing by 2.

$$ A = \frac{P \cdot r}{2} $$

If we express the perimeter as twice the semiperimeter, P = 2p, and simplify, we return to the original formula.

$$ A = \frac{2p \cdot r}{2} $$

$$ A = p \cdot r $$

This formula allows us to calculate the area (A) of the polygon using the radius (r) of the circle and the semiperimeter of the polygon.

Note: In a regular polygon, the radius of the circle is also referred to as the apothem or inradius.

Explanation

Let's consider a polygon circumscribed around a circle.

Take a hexagon, for example.

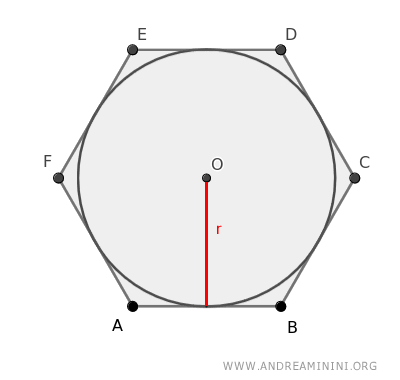
You can divide the hexagon into 6 triangles, each with one side (l) of the polygon as its base and the radius (r) of the circle as its height.

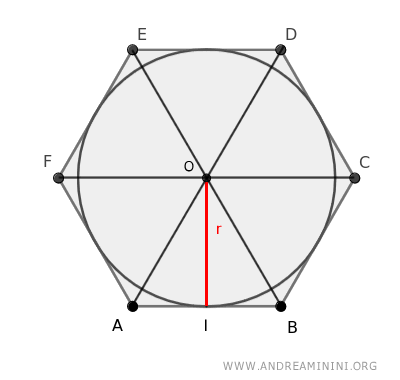
The area of each triangle is simply the base times the height divided by two, which in this case is the side length times the radius divided by 2.

$$ \frac{l \cdot r}{2} $$

Therefore, the area of the polygon is equal to the sum of the areas of these triangles.

$$ A = \frac{ \overline{AB} \cdot r }{2} + \frac{ \overline{BC} \cdot r }{2} + \frac{ \overline{CD} \cdot r }{2} + \frac{ \overline{DE} \cdot r }{2} + \frac{ \overline{EF} \cdot r }{2} + \frac{ \overline{AF} \cdot r }{2} $$

$$ A = \frac{ ( \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{EF} + \overline{AF} ) \cdot r }{2} $$

The sum in the numerator is simply the perimeter P of the polygon, so we have:

$$ A = \frac{ P \cdot r }{2} $$

Expressing the perimeter as twice the semiperimeter, P = 2p, and simplifying gives us:

$$ A = \frac{ 2p \cdot r }{2} $$

Which simplifies further to:

$$ A = p \cdot r $$

And that brings us back to the formula we set out to prove.

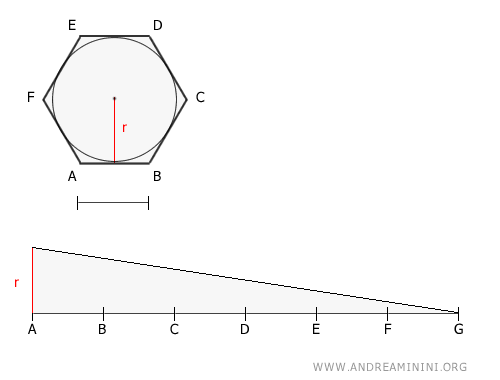
Geometric Proof: If we think of the perimeter as one leg of a right triangle and the radius as the other, the area of the triangle equals the area of the polygon.

Additional Notes

Here are a few additional observations:

• Inverse Formulas
  The area formula for a circumscribed polygon, $$ A = p \cdot r $$, can be used to derive some useful inverse formulas. For example, if you know the area (A) and the semiperimeter (p), you can find the radius: $$ r = \frac{A}{p} $$. Alternatively, if you know the area (A) and the radius (r), you can find the semiperimeter: $$ p = \frac{A}{r} $$.

And so on.