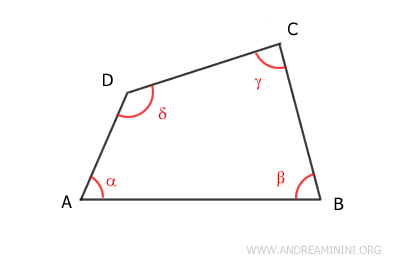
Quadrilaterals

A quadrilateral is a polygon with four sides.

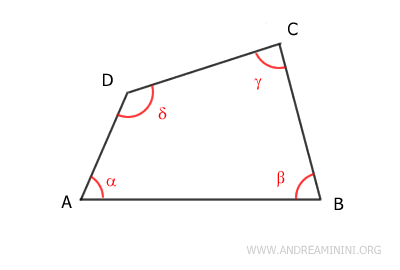
The sides of a quadrilateral can be categorized as:

• Adjacent sides
  if they share a common vertex.
• Opposite sides
  if they do not share any vertices.

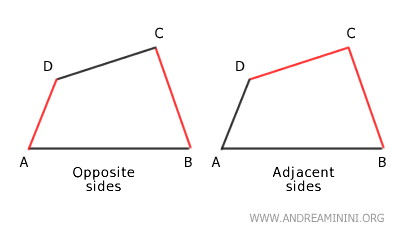
The angles in a quadrilateral can be:

• Adjacent angles
  if they share a common side.
• Opposite angles
  if they do not share any sides.

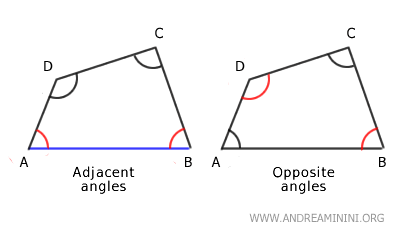
Every quadrilateral has two diagonals that connect the vertices of opposite angles.

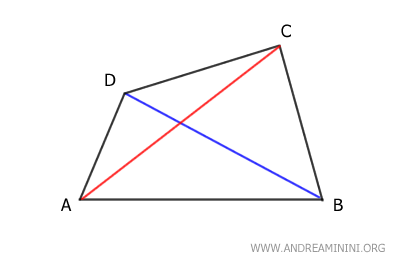
Note: A diagonal divides a quadrilateral into two triangles. Since the sum of the interior angles of a triangle is 180°, and a quadrilateral is composed of two triangles, the sum of the interior angles of a quadrilateral is 360°. 

The sum of the interior angles of a quadrilateral is always 360° (a full circle).

$$ \alpha + \beta + \gamma + \delta = 360° $$

Types of Quadrilaterals

Based on their shape, quadrilaterals can be classified into:

• Convex quadrilaterals
  All interior angles are less than 180° (convex), meaning that all of its diagonals lie within the quadrilateral.
  
  Convex quadrilaterals include trapezoids, parallelograms, and convex kites.
  • Trapezoids
    These are quadrilaterals with only one pair of parallel sides. A trapezoid can be scalene, isosceles, or right-angled.
    
  • Parallelograms
    These are quadrilaterals with opposite sides that are both parallel and equal in length.
    
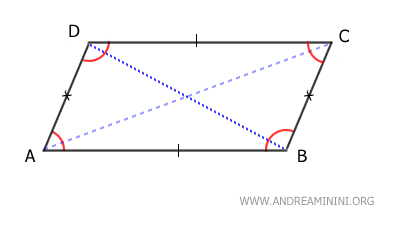
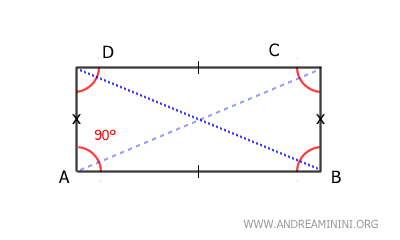
    Parallelograms include rectangles, rhombuses, and squares.
    • Rectangles
      Parallelograms with all angles at 90°.
      
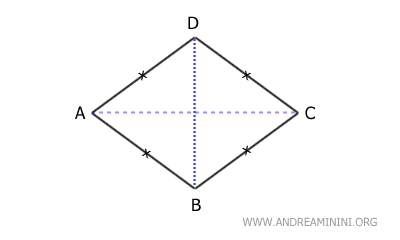
    • Rhombuses
      Parallelograms where all sides are of equal length and the diagonals are perpendicular.
      
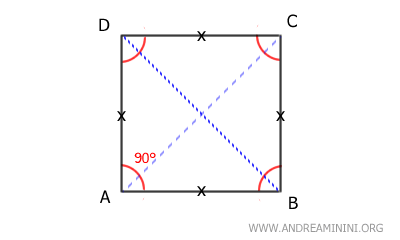
    • Squares
      Parallelograms with all sides of equal length, all angles at 90°, and perpendicular diagonals. In essence, squares possess the characteristics of both rectangles and rhombuses.
      
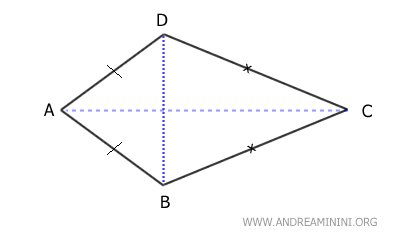
  • Convex kites
    These are quadrilaterals with perpendicular diagonals.
    
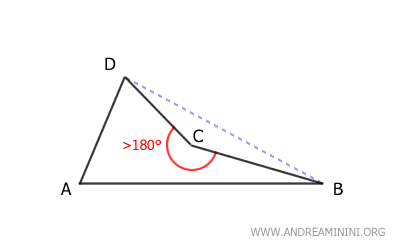
• Concave quadrilaterals
  In these quadrilaterals, at least one interior angle is greater than 180° (concave), meaning that at least one diagonal lies outside the quadrilateral.
  

Additional Notes

Some key points about quadrilaterals:

• The perimeter of a quadrilateral is the total length of all its sides.
• Each side of a quadrilateral is shorter than the sum of the other three sides.
• Area of a quadrilateral with perpendicular diagonals
  The area of a quadrilateral with perpendicular diagonals can be calculated by multiplying the lengths of the diagonals and dividing the result by two. $$ A = \frac{d_1 \cdot d_2}{2} $$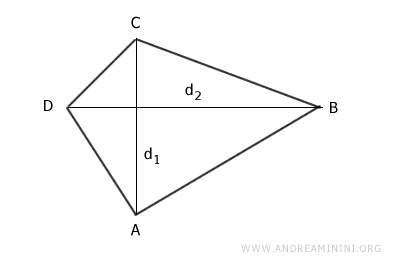

  

• Circumscribed Quadrilaterals
  A quadrilateral is circumscribed about a circle if the angle bisectors converge at a single point, known as the "incenter." The circle, centered at this incenter (O), touches all four sides of the quadrilateral.
  

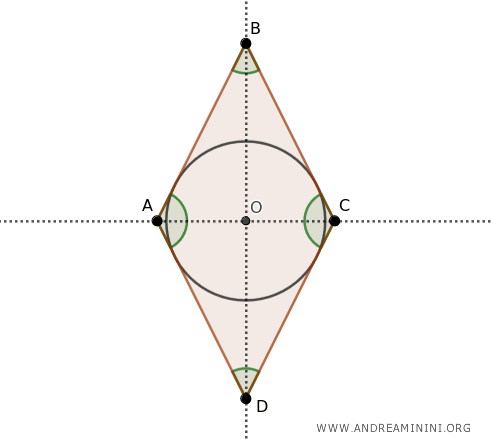
  For instance, a rhombus and a square are examples of quadrilaterals that can be circumscribed because their angle bisectors intersect at a common point. However, not all quadrilaterals have this property. Below is an example of a quadrilateral that cannot be circumscribed. 
  

  If a quadrilateral is circumscribed by a circle, the sum of the lengths of two opposite sides is equal to the sum of the lengths of the other two sides. $$ \overline{AB} + \overline{CD} = \overline{BC} + \overline{AD} $$

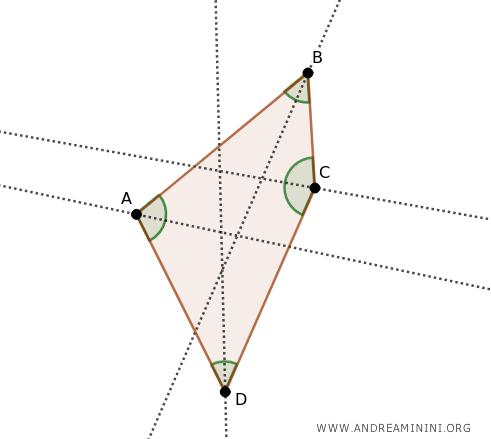
And so on...