Square

A square is a parallelogram with four equal sides and four right angles.

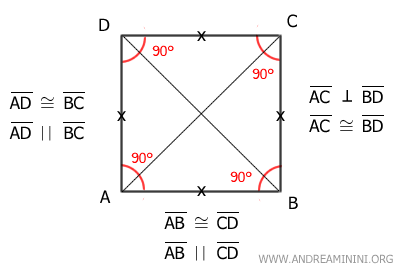
Alternatively, a square can be described as a parallelogram with four equal sides and angles. Therefore, a square is both a rhombus and a rectangle.

A square inherits all the properties of a rhombus:

• All sides of a rhombus are congruent
• The diagonals are perpendicular, forming a 90° angle
• The diagonals bisect the angles

It also inherits all the properties of a rectangle:

• Each angle is a right angle (90°)
• The diagonals are congruent, meaning they are of equal length

Formulas

Key formulas for a square

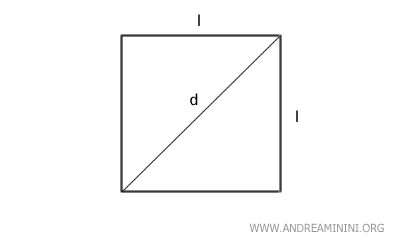
• Perimeter
  The perimeter of a square is four times the length of one side (l): $$ P = 4 \cdot l = l + l + l + l $$
• Area
  The area of a square is equal to the side length squared (l²): $$ A = l^2 $$ Alternatively, the area can be calculated as the square of the diagonal (d), divided by two: $$ A=\frac{d^2}{2} $$
• Diagonal
  The diagonal of a square is the product of the side length and the square root of 2: $$ d = l \cdot \sqrt{2} $$

  Note: This formula is derived from the Pythagorean theorem. The diagonal is the hypotenuse of a right triangle where the legs are two sides of the square: $$ d = \sqrt{l^2+l^2} $$ $$ d = \sqrt{2 \cdot l^2} $$ Simplifying, we obtain the earlier formula: $$ d = l \cdot \sqrt{2} $$
  

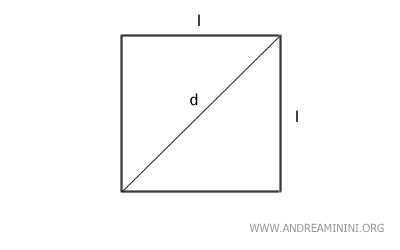
• Side Length
  The side length of a square can be found by dividing the perimeter by four: $$ l = \frac{p}{4} $$ or by taking the square root of the area: $$ l = \sqrt{A} $$ You can also determine the side length using the relationship between the side length and the radius of the circumscribed circle, by multiplying the radius by the square root of two: $$ l = r \cdot \sqrt{2} $$

  Note: This formula also comes from the Pythagorean theorem. The radii from the center of the circle (O) to two endpoints of a square side (l) form a 90° angle, creating a right triangle where the legs are the radius and the hypotenuse is the side of the square. $$ l = \sqrt{r^2+r^2} $$ $$ l = \sqrt{2r^2} $$ Simplifying gives us the desired formula: $$ l = r \cdot \sqrt{2} $$
  

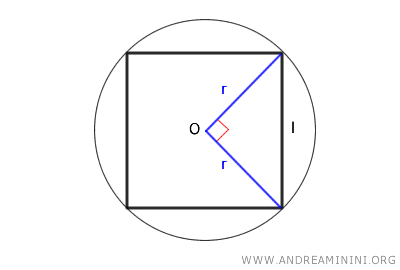
• The side length of a square is twice the radius of the inscribed circle: $$ l = 2r $$

  Note: This formula is fairly intuitive. The diameter (2r) of the inscribed circle is equal to the sides of the square. This is because the diameter of the inscribed circle touches the sides of the square at four points of tangency (one per side), making the circle the largest possible that can fit inside the square without exceeding its boundaries.
  
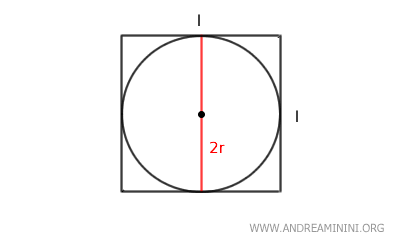
  It can also be demonstrated that there is a relationship between the radius of the inscribed circle and the side length of the square.

How to Draw a Square

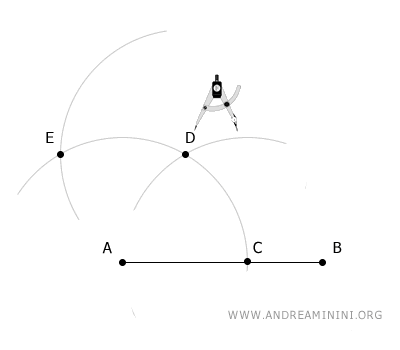
Begin by drawing line segment AB as the first side of the square.

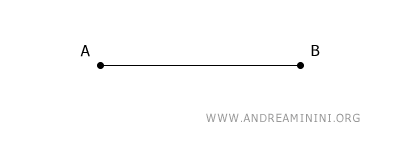
Place the compass at point A and draw an arc with any desired radius.

The arc intersects segment AB at point C.

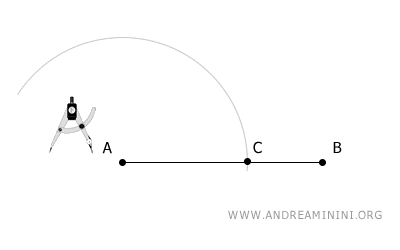
Using the same radius, place the compass at point C and draw a second arc that intersects the first arc at point D.

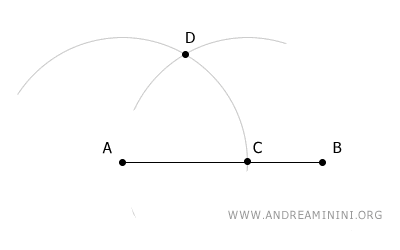
Next, place the compass at point D, again using the same radius, and draw a third arc that intersects the first arc at point E.

Finally, place the compass at point E and, with the same radius, draw an arc that intersects the last arc at point F.

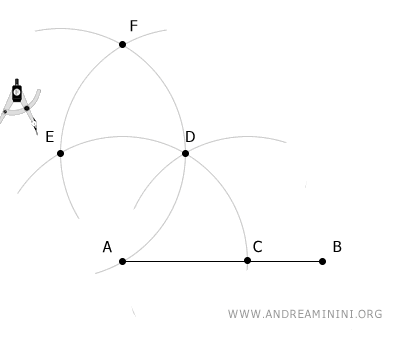
Now, draw a line between points A and F.

This line is perpendicular to AB and passes through point A.

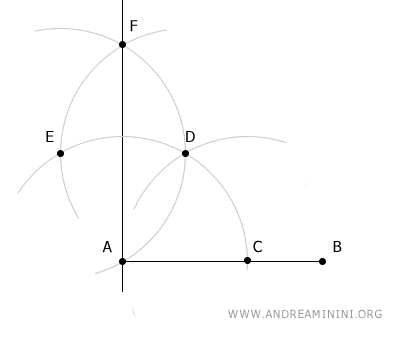
Place the compass at point A and, with a radius equal to AB, draw an arc that intersects the perpendicular line at point F.

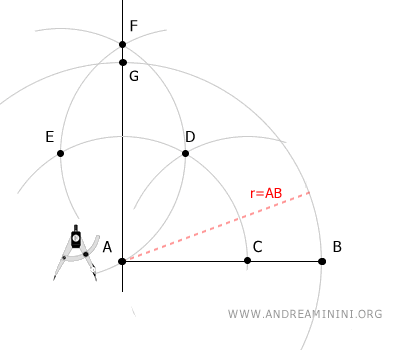
Maintaining the same radius, place the compass at point G and draw another arc.

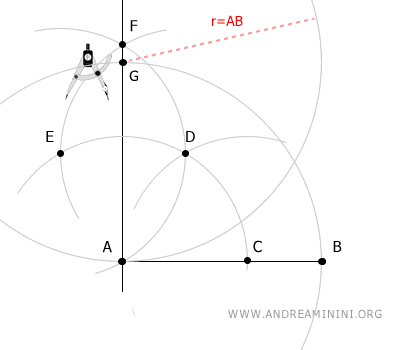
Finally, using the same radius, place the compass at point B and draw an arc that intersects the last arc at point H.

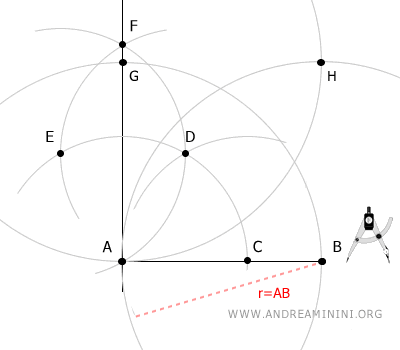
Connect points A, B, G, and H with line segments.

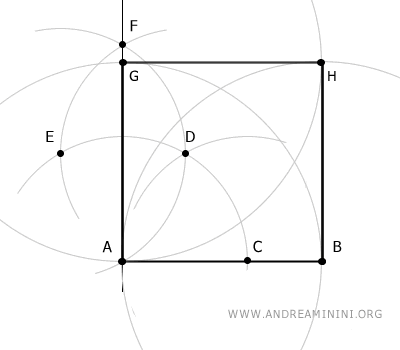
The resulting figure ABHG is a square.

Alternatively, you can also draw a square inscribed in a circle.

Observations

Some observations and notes on squares

• A square has congruent diagonals

  Proof: A square ABCD, by definition, has equal sides and equal angles (right angles). Based on this, we can state that triangles ABD and ABC are congruent by the side-angle-side (SAS) congruence theorem because they share a common side (AC), have congruent sides (AB≅BC), and the included angle is congruent (90°), which is a right angle.
  
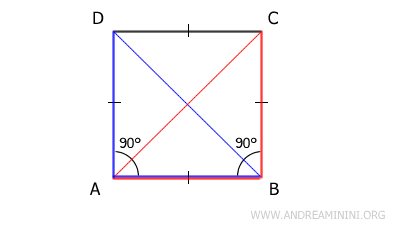
  Congruent triangles ABD≅ABC have all corresponding sides and angles congruent in the same order. Specifically, their hypotenuses AC and BD are congruent (AC≅BD) because they are also the diagonals of the square. Therefore, the diagonals of a square are congruent.

• A parallelogram is a square if its diagonals are congruent and perpendicular

  Proof: Given that parallelogram ABCD has congruent diagonals AC≅BD that are also perpendicular, the diagonals intersect at their midpoint M. Therefore, the half-diagonals AM, BM, CM, and DM are congruent.
  
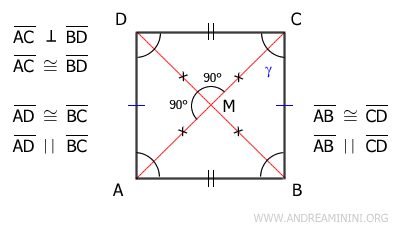
  From this, we can deduce that triangles AMD and CDM are congruent by the side-angle-side (SAS) congruence theorem because they share a common side DM, have congruent sides AM≅CM, and the included angle is congruent (90°). Hence, triangles AMD≅CDM have all sides and angles congruent.
  
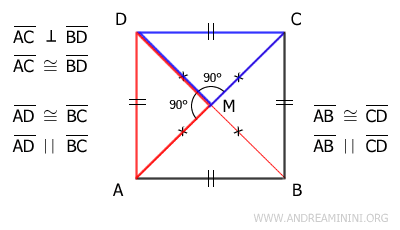
  What is most relevant here is that their hypotenuses AD≅CD are congruent because AC and CD are two consecutive sides of the parallelogram. Since opposite sides of a parallelogram are congruent, we deduce that all sides of the parallelogram are congruent, meaning they are of equal length. Given that the diagonals are congruent, we can conclude that the figure is a square, not a rhombus.

• A diagonal divides a square into two isosceles right triangles

  Proof: By definition, a square ABCD has equal sides and angles (right angles). A diagonal, such as AC, divides the square into two right triangles because one of the angles is necessarily a right angle (90°). The two triangles are also isosceles because two of their sides (AB≅BC and AD≅CD) are equal as given in the initial hypothesis.
  
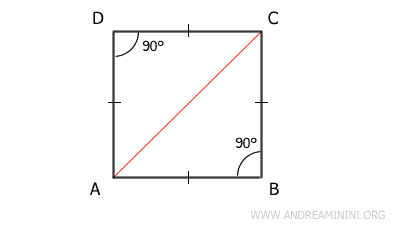
  The same result is obtained by analyzing the other diagonal BD of the square. For the same reasons, the diagonal divides the square into two isosceles right triangles.
  

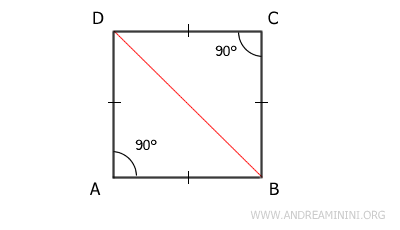
• The two diagonals divide the square into four isosceles triangles

  Proof: The square ABCD is a parallelogram with equal sides and angles. In all parallelograms, the diagonals intersect at their midpoint M.
  
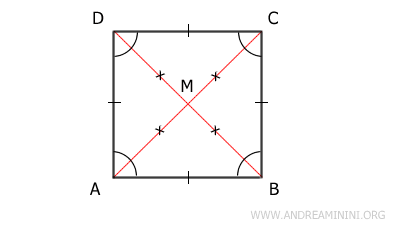
  Unlike other parallelograms, in a square, the diagonals are also congruent. This means the square can be divided into four triangles with two congruent sides, or four isosceles triangles: ABM, BCM, CDM, and ADM. Since the diagonals of a square are also perpendicular to each other, these four triangles are not only isosceles but also right triangles.

• A parallelogram is a square if its diagonals are congruent and one diagonal bisects an angle

  Proof: In parallelogram ABCD, let’s assume the diagonals AC≅BD are congruent, and one diagonal bisects an angle. For instance, diagonal AC bisects the angle at vertex A, making angles α' and α'' congruent (α'≅α'').
  
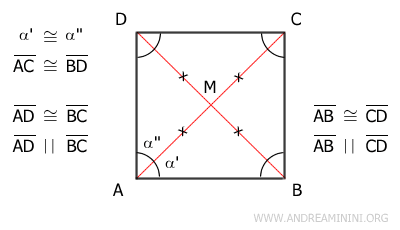
  Since it’s a parallelogram, the opposite sides are congruent (AB≅CD and AD≅BC) and parallel (AB||CD and AD||BC). Therefore, diagonal AC can be considered as a transversal between two parallel lines AD and BC. Consequently, according to the parallel lines theorem, the alternate interior angles α''≅γ are congruent.
  
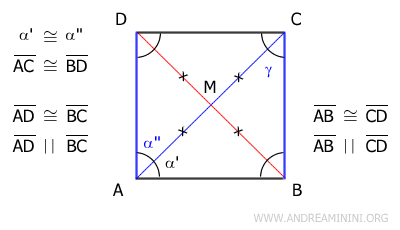
  Since α'≅α'' are congruent by the initial hypothesis, we can also conclude that α'≅γ are congruent. This means that triangle ABC is an isosceles triangle because it has two congruent angles at the base AC. Being an isosceles triangle, its two sides AB≅BC are congruent. Consequently, since they are two consecutive sides of the parallelogram, we can state that all sides of the parallelogram are congruent.
  
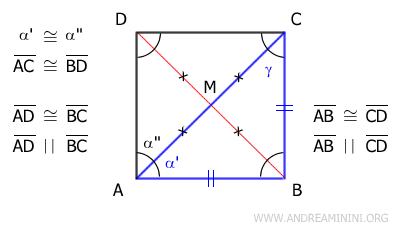
  The final step is to determine whether the parallelogram is a rhombus or a square. This is easily resolved by noting that the diagonals are congruent, which confirms that the figure ABCD is indeed a square.

And so on.