Relationship Between the Side of a Square and the Radius of Its Inscribed Circle
The side of a square is equal to twice the radius (or the diameter) of its inscribed circle. $$ l = 2r $$ 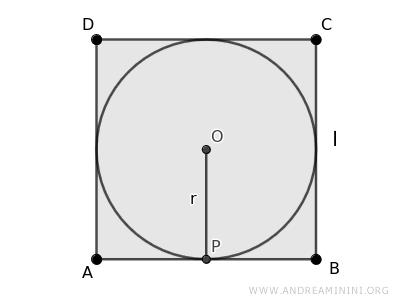
As a corollary, we can deduce that the radius of the inscribed circle is half the length of the square’s side.
$$ r = \frac{l}{2} $$
This may seem obvious, but it’s worth stating explicitly.
The proof that the diameter of an inscribed circle in a square is congruent to the square’s side length is quite straightforward, as it relies on basic geometric principles.
Proof
Consider a square ABCD with an inscribed circle.
In a square, the center O of the inscribed circle coincides with the center of the square.
Let’s label this center \(O\) and the radius of the circle \(r\).
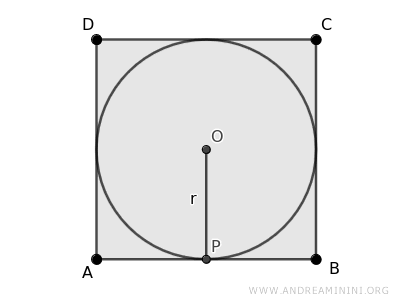
The inscribed circle touches each side of the square at exactly one point of tangency: \(P\), \(Q\), \(R\), and \(S\).
Since these are points of tangency, the radii OP, OQ, OR, and OS are perpendicular to the sides of the square, forming right angles (90°).
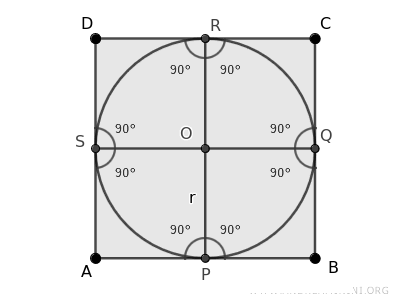
Next, we draw the diagonals of the square.
In a square, the diagonals are congruent and bisect each other.
The center O of the inscribed circle lies at the intersection of the square’s diagonals, which is also the center of the square itself.
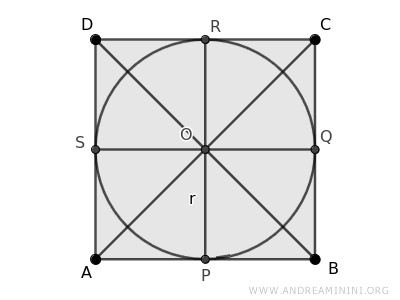
The diagonals divide the square into eight triangles: AOP, AOS, BOP, BOQ, COQ, COR, DOR, and DOS.
These eight triangles are:
- Right triangles because the radii OP, OQ, OR, and OS are perpendicular (90°) to the sides of the square.
- Isosceles triangles because they have two congruent angles (45°). Thus, their non-right sides are congruent.
Note: The central angle at O (360°) is divided into eight congruent angles of 45° each. Additionally, the diagonals bisect each 90° angle of the square into two congruent 45° angles.
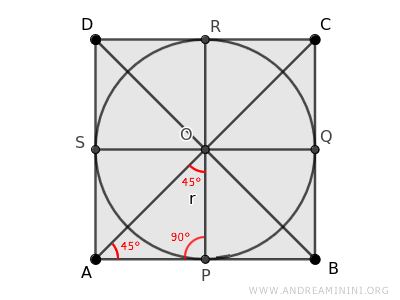
- Congruent triangles because, according to the first criterion of triangle congruence, they have congruent non-right sides (the radius and half the side of the square) and a congruent angle between them (90°).
Since these triangles are congruent, we can focus on just one of them, for example, triangle AOP.
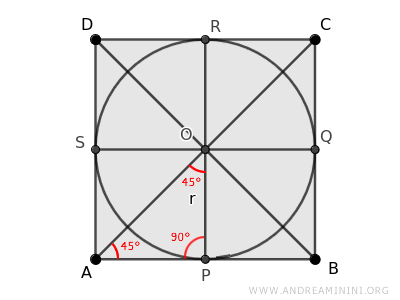
To summarize, triangle AOP is an isosceles triangle, so its non-right sides AP ≅ OP are congruent.
$$ \overline{AP} = \overline{OP} $$
The segment OP = r is the radius of the inscribed circle.
$$ \overline{AP} = r $$
The segment AP is half the side L of the square.
$$ \frac{L}{2} = r $$
Multiplying both sides of the equation by two, we get:
$$ \frac{L}{2} \cdot 2 = r \cdot 2 $$
$$ L = 2r $$
This proves that the diameter of the inscribed circle \(2r\) is equal to the side length of the square \(L\).
And so on.
