Equidecomposable Polygons

Two or more polygons are called equidecomposable polygons or equicomposable polygons when they can be divided into congruent smaller polygons.

In other words, two polygons are equidecomposable if they can be split into a finite number of parts (smaller polygons), and each part of one polygon is congruent to a part of the other polygon, and vice versa.

This means we can rearrange the parts of one polygon to form the other polygon.

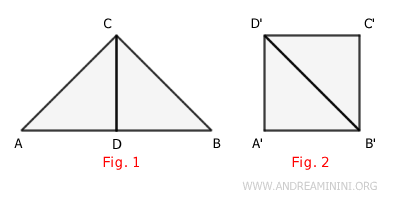
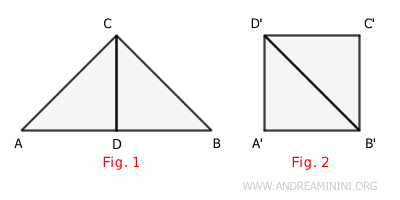
For example, if I have two polygons (Figure 1 and Figure 2) and I can decompose the first one into parts that can be reassembled to form the second polygon, and vice versa, then they are equidecomposable polygons.

the figures are equivalent

Note: This concept is closely related to Cavalieri's principle, which states that if two solid figures in three-dimensional space are arranged so that every plane parallel to a fixed plane intersects both figures in cross-sections of equal area, then the two figures have the same volume.

A Practical Example
Observations

A Practical Example

Consider two polygons: Figure 1 and Figure 2.

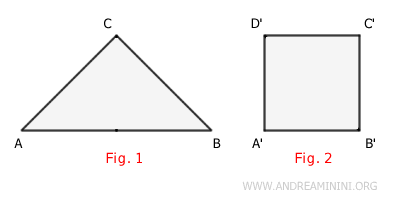
two polygons

I decompose the polygon in Figure 1 into two parts, each of which is a smaller polygon (ACD and BCD).

Figure 1 is decomposed into two polygons

The sum of the areas of the component polygons is equal to the area of the original polygon A.

$$ Area(ABC) = Area(ACD) + Area(BCD) $$

I then reassemble the two parts differently, without overlapping them, to exactly cover the surface of polygon B.

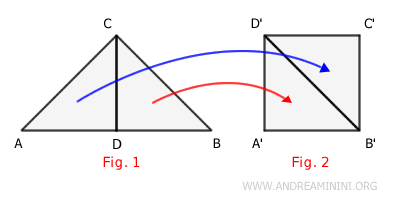
the two figures are equidecomposable

From this, I deduce that the two polygons A and B can be decomposed into the same congruent polygons and, therefore, have the same area (equivalent areas), meaning they cover the same space.

$$ ACD \cong B'C'D' $$ $$ BCD \cong A'B'D' $$

Essentially, they are composed of the same partition of polygons.

the figures are equivalent

Since they have the same surface area, they have the same total area, which is the sum of the areas of the component polygons.

In this case, they are called equidecomposable.

Observations

Here are some additional notes on equidecomposable polygons:

Two polygons are equidecomposable even if they are the difference of congruent polygons
The same considerations apply as for the sum of congruent polygons.
Two equidecomposable polygons have the same area, meaning they have equivalent surfaces
For this reason, they are also called equivalent polygons.
Equidecomposability is an equivalence relation
Therefore, the same mathematical properties satisfied by equivalence relations hold. Surfaces with the same area belong to the same equivalence class.
Two equidecomposable polygons are equivalent polygons
When two polygons are composed of the same parts, they are equivalent polygons because they have the same area.
Dehn's Theorem
Two equidecomposable figures are also geometrically equivalent, but the converse is not necessarily true.
Example: In the plane, two equivalent polygons have the same area and are composed of the same equivalent surfaces, so they are always equidecomposable. Conversely, in space, two polyhedra with the same volume are not necessarily equidecomposable.
The concept of equidecomposability in the history of geometry and mathematics
The concept of equidecomposability has important implications in measure theory, especially in the context of the equivalence of geometric figures in terms of area or volume, and in understanding and proving the properties of geometric figures.
Example: A famous example is the Greek square problem, which deals with the possibility of dividing a square into pieces that can be rearranged to form a circle of equal area. This question has led to the development of measure theory and modern integral calculus over the centuries.

And so on.