Hexagon

A hexagon is a closed geometric figure with six sides and six angles.

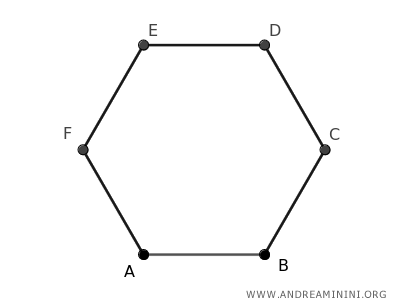
When a hexagon has sides and angles that are all equal, it’s specifically called a regular hexagon.

Each interior angle of a regular hexagon measures 120°.

There are also irregular hexagons, where the sides have different lengths and the angles are not congruent.

For the rest of these notes, when I mention a "hexagon," I'll be referring to a regular hexagon.

Formulas

Here are the key formulas you need to know for calculating the perimeter (P) and area (A) of a hexagon:

• Perimeter
  The perimeter of a regular hexagon is six times the length of one side (l): $$ P = 6 \cdot l $$
• Area
  The area of a regular hexagon can be calculated if you know the apothem (a): $$ A = \frac{P \cdot a}{2} \ \ \text{or} \ \ A = 2.598 \cdot l^2 $$ where $ l $ is the side length, and $ a $ is the apothem of the hexagon. $$ a = 0.866 \cdot l $$
• Side Length
  The side length of a regular hexagon is equal to the radius of the circumscribed circle (proof): $$ l = r $$ Alternatively, you can calculate the side length if you know the radius (r) of the inscribed circle (proof): $$ l = \frac{2\sqrt{3}}{3} \cdot r $$ Or, knowing the apothem (a), which is the same as the radius of the inscribed circle (r=a): $$ l = \frac{2\sqrt{3}}{3} \cdot a $$

Perimeter

The perimeter of a hexagon is simply the side length multiplied by six.

$$ P = 6 \cdot l $$

Sometimes the symbol "2p" is used to represent the perimeter, where "p" is lowercase.

$$ 2p = 6 \cdot l $$

This is because the lowercase "p" represents the semiperimeter of a polygon.

$$ p = \frac{P}{2} $$

In contrast, the uppercase "P" is used to denote the full perimeter. So, P=2p.

Example: Consider a regular hexagon with a side length of l=2.

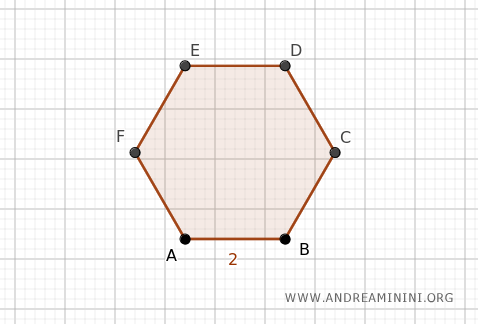
Since a hexagon has n=6 sides, its perimeter is P=12 $$ P = n \cdot l = 6 \cdot 2 = 12 $$ Therefore, its semiperimeter is simply half of the perimeter, which is p=6 $$ p = \frac{P}{2} = \frac{12}{2} = 6 $$

Apothem

The apothem (a) of a hexagon is the radius of the inscribed circle.

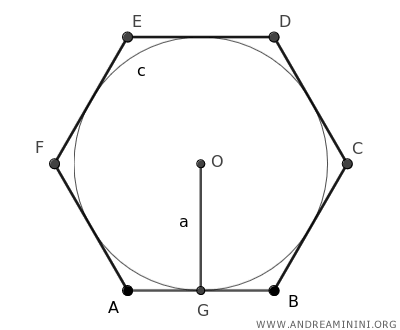
You can find it by drawing a line segment (OG) from the center (O) to the midpoint of any side of the hexagon, at the shortest distance.

In geometric terms, the apothem is the perpendicular distance from the center of the hexagon to one of its sides.

The formula to calculate the apothem from the side length "l" is:

$$ a = l \cdot f_1 $$

Where f₁ is a constant value for hexagons, equal to f₁=0.866.

What are fixed numbers? In a regular hexagon, the ratio of the apothem "a" to the side length "l" is a constant value of 0.866 $$ f_1 = \frac{\sqrt{3}}{2} = 0.866 $$ This value is known as a "fixed number" because it remains constant regardless of the size of the hexagon.

What is it used for?

The apothem is useful for various geometric calculations, such as finding the area of the hexagon.

Hexagon Area

The area of a regular hexagon can be calculated by multiplying the semiperimeter (p) by the apothem (a).

$$ A = p \cdot a $$

Here, "p" (lowercase) represents the semiperimeter, while P=2p (uppercase) is the full perimeter. Therefore, the semiperimeter is p=P/2.

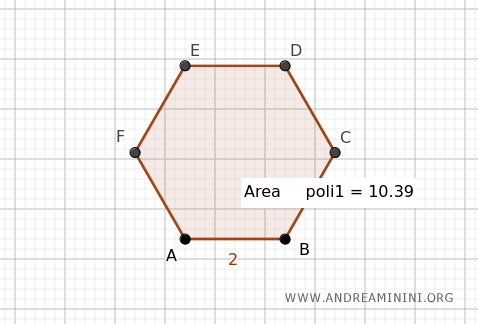
Example: A regular hexagon has a side length of l=2.

So, with n=6 sides, its perimeter is P=12 $$ P = n \cdot l = 6 \cdot 2 = 12 $$ Thus, its semiperimeter is p=6 $$ p = \frac{P}{2} = \frac{12}{2} = 6 $$ Now, calculate the hexagon's apothem: $$ a = 0.866 \cdot l = 0.866 \cdot 2 = 1.732 $$ Finally, find the area of the hexagon using p=6 and a=1.732: $$ A = p \cdot a = 6 \cdot 1.732 = 10.392 $$ The area of the hexagon is 10.392.

Alternative Method for Calculating Area

You can also calculate the area of the hexagon using the fixed numbers associated with hexagons.

$$ A = l^2 \cdot f_2 $$

Here, "l" is the side length, and f₂ is a constant value for hexagons, f₂=2.598.

Example: Let’s consider the same regular hexagon from the previous example, with a side length of l=2.

To find the area, multiply the square of the side length by the fixed number f₂=2.598: $$ A = l^2 \cdot f_2 = 2^2 \cdot 2.598 = 4 \cdot 2.598 = 10.392 $$ The area of the hexagon is 10.392, which matches the result from the previous method.

Hexagon Fixed Numbers

The fixed numbers for a hexagon are f₁=0.866 and f₂=2.598. $$ f_1 = \frac{a}{l} = 0.866 $$ $$ f_2 = 2.598 $$ These are particularly useful for calculating the apothem and the area of a hexagon.

There is a relationship between the two fixed numbers, f₁ and f₂.

We know that the area of a hexagon is the product of the semiperimeter (p) and the apothem (a):

$$ A = p \cdot a $$

In a regular hexagon, the ratio of the apothem (a) to the side length (l) is a constant value of 0.866.

$$ f_1 = \frac{a}{l} = 0.866 $$

Note: Sometimes, the fixed number f₁ is also expressed as the square root of 3 divided by 2: $$ f_1 = \frac{\sqrt{3}}{2} = 0.866 $$ This ratio comes from the fact that a hexagon can be divided into six equilateral triangles.

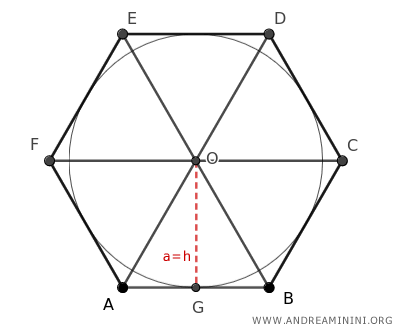
The height (h) of each equilateral triangle that forms the hexagon coincides with the apothem (a): $$ a = h $$ Knowing that the height (h) of an equilateral triangle is the product of the side length (l) and a constant value of √3/2: $$ h = \frac{\sqrt{3}}{2} \cdot l $$. Considering a unit side length l=1, we get the fixed number f₁=0.866: $$ a=h=\frac{\sqrt{3}}{2} = 0.866 $$

Thus, the apothem of a hexagon is a=l·0.866

$$ A = p \cdot a $$

$$ A = p \cdot (l \cdot 0.866) $$

The semiperimeter p=P/2 is half of the perimeter of the hexagon.

$$ A = \frac{P}{2} \cdot (l \cdot 0.866) $$

In turn, the perimeter P=nl is equal to the product of the number of sides (n=6) and the side length "l".

$$ A = \frac{nl}{2} \cdot l \cdot 0.866 $$

$$ A = \frac{6 \cdot l}{2} \cdot l \cdot 0.866 $$

$$ A = \frac{6 \cdot 0.866}{2} \cdot l^2 $$

$$ A = 2.598 \cdot l^2 $$

Here, 2.598 is the fixed number f₂ of the hexagon.

Additional Notes

Here are some additional observations and notes about hexagons:

• Constructing a Regular Hexagon
  A regular hexagon can be drawn using only a straightedge and compass.
  
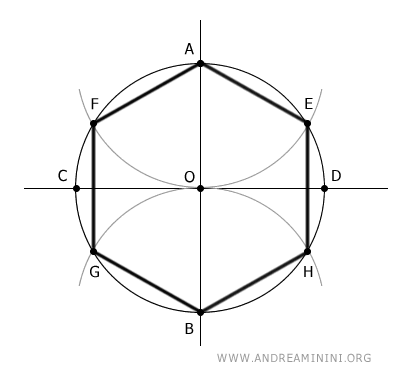
• The Side Length of a Regular Hexagon Equals the Radius of the Circumscribed Circle
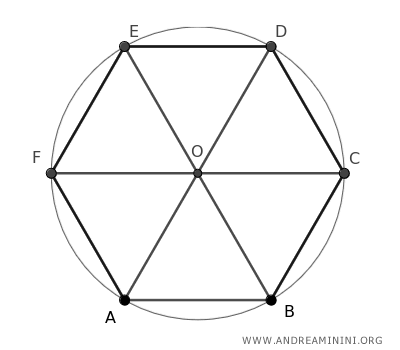
  The side length of a regular hexagon is equal to the radius of the circumscribed circle. This occurs because each triangle that has the hexagon’s side as its base, and the circle’s radii as its oblique sides, is an equilateral triangle.
  
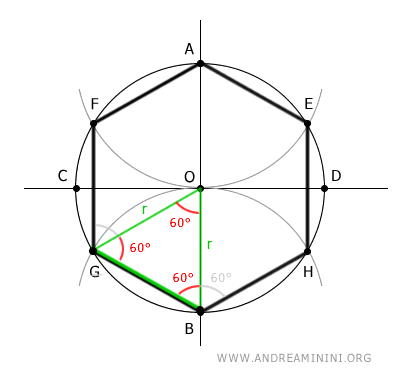
• The Side of the Hexagon is Related to the Radius of the Inscribed Circle and the Apothem
  The side length of a regular hexagon is related to the radius of the inscribed circle (r) and the apothem (a), which coincides with the radius (r=a) in this case, through the following formula: $$ l = \frac{2\sqrt{3}}{3} \cdot r $$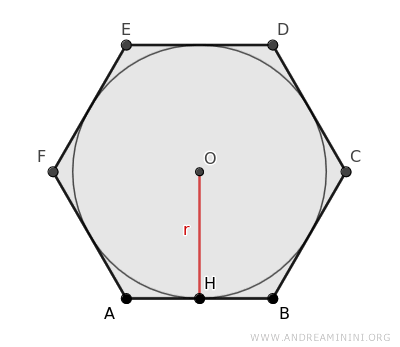
• Space Optimization
  Among polygons, the regular hexagon stands out for its harmony and symmetry. All sides are equal, and the internal angles are identical. This uniformity creates a sense of visual balance and structural stability. The ability of regular hexagons to fit together perfectly without leaving gaps is the basis for tessellations.
  
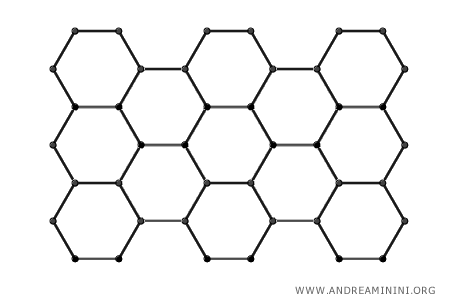
  For this reason, hexagons are often used to optimize space. For example, in architecture and engineering, hexagonal cells are employed in building design. In biology, hexagons are the shape used by bees to construct hives, and in economic geography, hexagons are utilized to study localization patterns.
• The Side of a Hexagon is Congruent with the Radius of the Circumscribed Circle
  The side length of a hexagon is the same as the radius of the circumscribed circle. This property is due to the fact that a hexagon can be divided into six equilateral triangles.
  
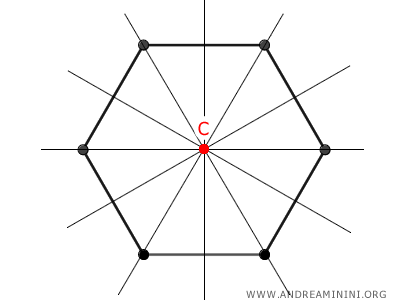
• A hexagon has a center of symmetry and six axes of symmetry that pass through the center
  

And so on.