The Side of a Hexagon Equals the Radius of Its Circumscribed Circle

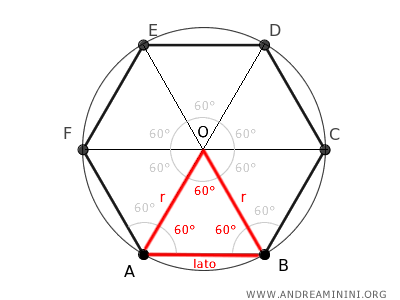
The length of a side of a regular hexagon is exactly the same as the radius of the circle that circumscribes the hexagon.

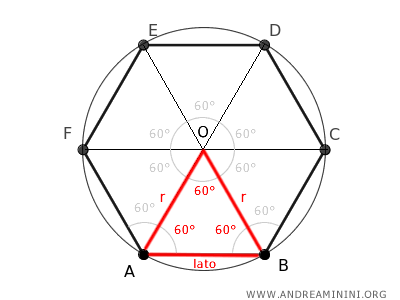
This is because a regular hexagon can be divided into six congruent equilateral triangles.

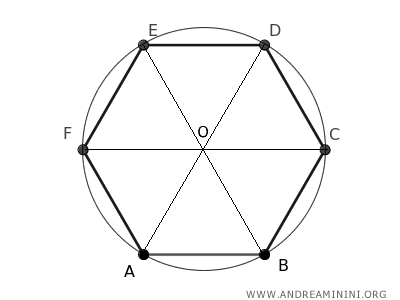
Each triangle has a base that forms a side of the hexagon, and the other two sides are radii extending from the center of the hexagon, which is also the center of the circumscribed circle, to the vertices of the hexagon.

These triangles are equilateral because all their sides and angles are congruent.

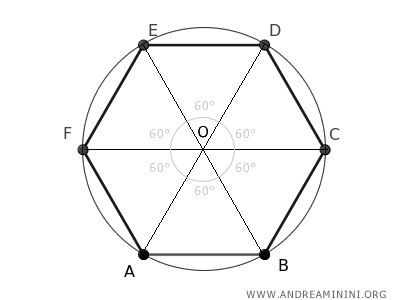
The full 360° angle at the center O is divided into six equal parts, creating six 60° angles.

So, the angle opposite the base of each triangle is 60°.

Since each interior angle of a regular hexagon measures 120°, the angles adjacent to the base of the triangles must also be 60°.

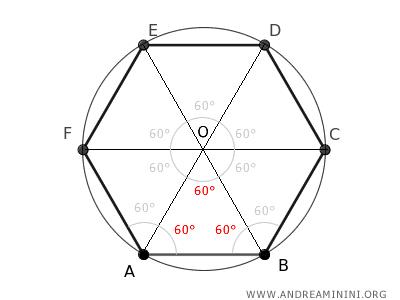
This shows that all the triangles that make up the hexagon are equilateral triangles because each of their angles is 60°.

The base of each triangle is also a side of the hexagon, while the two other sides are the radii of the circle.

Since all sides of an equilateral triangle are equal, it follows that the radius (which is one of the sides of the triangle) is equal to the length of a side of the hexagon.

This property of regular hexagons makes them especially useful in various geometric proofs and practical applications.

And so on.