Polygons
A polygon is a plane figure defined by a closed, non-intersecting broken line and all the points within it.
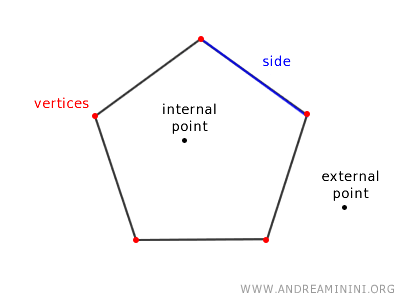
The segments that make up this closed broken line (or closed polygonal line) are called the sides of the polygon.
The endpoints of the sides are referred to as the vertices of the polygon.
Typically, the sides of a polygon are labeled with lowercase letters, while the vertices are labeled with uppercase letters.
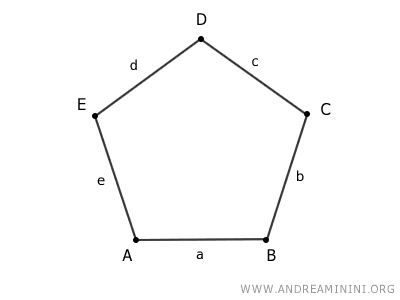
The word "polygon" comes from the ancient Greek words πολύς (polys, "many") and γωνία (gōnia, "angle"), meaning "many angles." In plane geometry, a polygon has at least three sides because a closed broken line requires at least three distinct points (vertices).
Each vertex of a polygon has an interior angle and an exterior angle.
The points on the closed broken line are called the perimeter of the polygon.
The points inside the closed broken line are called interior points, while those outside are called exterior points.
Polygon Classification
There are various ways to classify polygons.
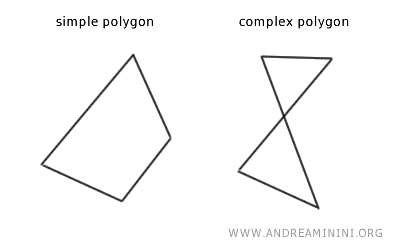
Generally, a polygon is called a "simple polygon" if its non-consecutive sides do not intersect.
If they do intersect, it is called a "complex polygon" (or "self-intersecting polygon").
Another classification is based on the congruence of its sides and angles.
A polygon is called a regular polygon if all its angles and sides are congruent, meaning they are of equal length.
If not, it is called an irregular polygon.
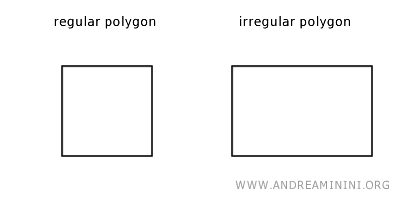
For example, a square is a regular polygon because all its sides and angles are congruent, while a rectangle is an irregular polygon because its sides are not all the same length. Similarly, an equilateral triangle is a regular polygon, while a scalene triangle is an irregular polygon.
There are also classifications based on the concavity or convexity of the shape or the number of angles.
Concave and Convex Polygons
A polygon can be either convex or concave.
- Convex Polygons
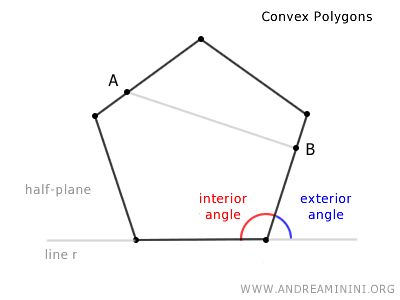
A convex polygon is a shape where, for any two points A and B, the segment AB connecting them lies entirely within the polygon. In other words, there are no external points on the segment. Convex polygons have all their interior angles less than 180 degrees.

Note: A convex polygon has all convex angles. Additionally, if you consider a line that includes one of its sides, the polygon is entirely contained within one of the two half-planes defined by the line.
- Concave Polygons
A concave (non-convex) polygon is a shape where there exist at least two points A and B such that the segment AB connecting them does not lie entirely within the polygon. In other words, some points on the segment lie outside the polygon.
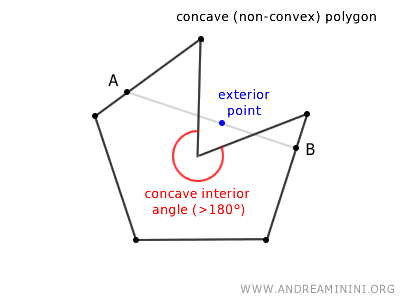
Note: A concave polygon must have at least four sides. Additionally, at least one of its interior angles must be greater than 180 degrees, meaning there must be at least one concave interior angle.
Types of Polygons
Polygons have different names based on the number of angles.
| Polygon | Angles |
|---|---|
| Triangle | 3 angles |
| Quadrilateral | 4 angles |
| Pentagon | 5 angles |
| Hexagon | 6 angles |
| Heptagon | 7 angles |
| Octagon | 8 angles |
| Nonagon | 9 angles |
| Decagon | 10 angles |
| Hendecagon | 11 angles |
| Dodecagon | 12 angles |
Diagonals and Chords of a Polygon
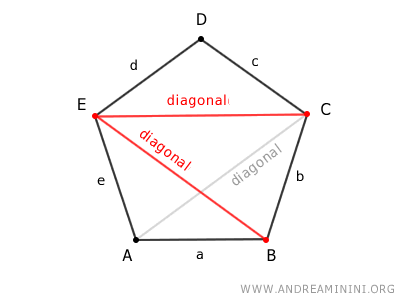
A diagonal of a polygon is a segment that connects two non-adjacent vertices.
For example, segments EC and EB are two diagonals of the polygon.
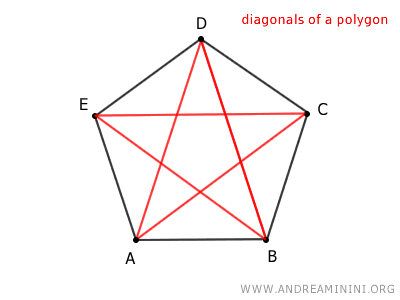
How many diagonals does a polygon have? A polygon with n vertices has n·(n-3)/2 diagonals. $$ \frac{n \cdot (n-3)}{2} $$ For example, a pentagon has n=5 sides, so it has 5 diagonals: $$ \frac{5 \cdot (5-3)}{2} = \frac{5 \cdot 2}{2} = \frac{10}{2} = 5 $$ To verify this, simply draw all the diagonals of the pentagon and count them.
A chord of a polygon is a segment that connects any two points on the perimeter that are not on the same side.
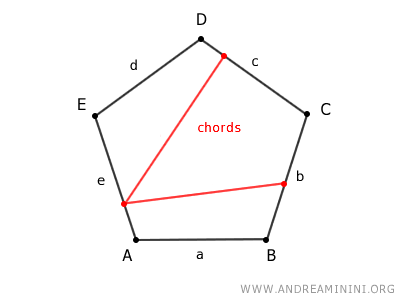
Every polygon has an infinite number of chords because the points that make up the perimeter of a geometric figure are infinite.
Observations
Here are some observations, properties, and notes on polygons.
- Two polygons are congruent if they can be superimposed with a rigid motion
Congruent polygons have congruent sides and angles in the same order, meaning they have the same measurements. - Perimeter of a polygon
The perimeter of a polygon is equal to the sum of the lengths of its sides. - The sum of the interior angles of a polygon with n sides is given by the formula $$ (n−2) \cdot 180° $$
For example, a square has n=4 sides. Therefore, the sum of its interior angles is 360°. $$ (4−2) \cdot 180° = 2 \cdot 180° = 360° $$ Indeed, a square has four right angles (90° each).
- A polygon with n sides has n vertices and n angles.
Each side of a polygon ends at two vertices. However, since each vertex is shared by two sides, the total number of vertices is the same as the number of sides. Similarly, each vertex has an associated angle, so the number of angles is also equal to the number of sides.
And so on.
