Interior Angles

Interior angles are the angles formed where two adjacent sides of a polygon intersect.

For example, let's consider a triangle ABC:

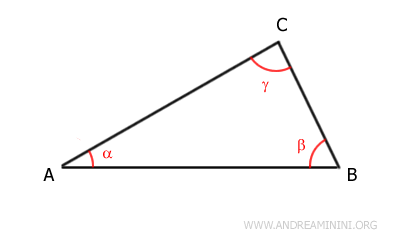
This triangle has three interior angles: α, β, and γ.

• The angle α is between side AB and the adjacent side AC.
• The angle β is between side AB and the adjacent side BC.
• The angle γ is between side BC and the adjacent side AC. 

Key Points

Here are some important points about interior angles:

• Sum of interior angles
  In a polygon with n sides, the sum of the interior angles is always (n-2)·180°. $$ (n-2) \cdot 180° $$

  Example: A square has n=4 sides and thus 4 interior angles. The sum of these angles is always 360° because $$ (n-2) \cdot 180° = (4-2) \cdot 180° = 2 \cdot 180° = 360° $$

• Relationship between interior and exterior angles
  In any polygon, an interior angle and its corresponding exterior angle always add up to 180°.

And so forth.