Comparing Angles

One of the classic methods used to compare the sizes of two angles is the superposition method.

1. To compare two angles, α and β, to determine if they are congruent:
   
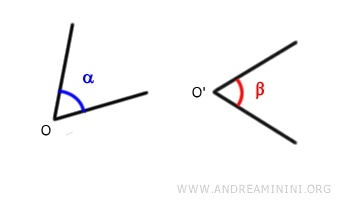
2. First, align the vertex O of the first angle (α) with the vertex O' of the second angle (β) by translation:
   
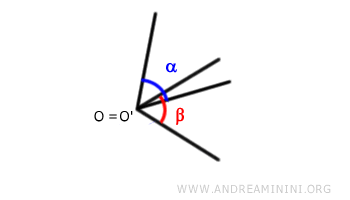
3. Next, rotate one side of the first angle (α) to overlap with one side of the second angle (β):
   
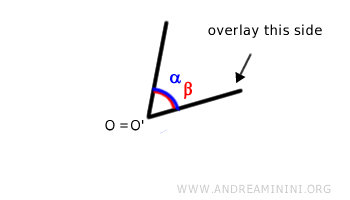
4. If the other two sides also overlap, the two angles are congruent α≅β, meaning they have the same size measured in degrees or radians:
   
   

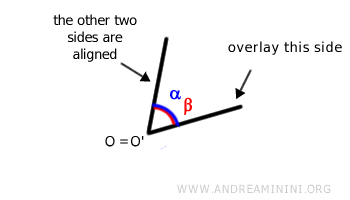
   Conversely, if the other two sides do not overlap, the angles are not congruent. In this case, one angle is larger and the other is smaller. An angle is smaller if it is contained within the angular region of the other angle. Otherwise, it is larger. For example, consider two other angles, α and β, and overlay them using the same procedure described above:
   
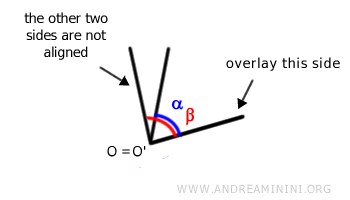
   In this example, angle α (blue) is entirely within the angular region of angle β (red). Therefore, angle α is smaller than angle β. Thus, we can say that angle α is smaller than β or angle β is larger than α.

The Difference Between Congruent and Equal Angles

More precisely, when two angles can be superimposed in geometry, we refer to them as "congruent angles" rather than "equal angles", because equality implies that the angles share the same points on the plane, which is not always the case.

Congruence, on the other hand, does not imply that two geometric objects share the same points in space.

For example, two angles α and β may have the same measure in degrees or radians (e.g., 90°) but be located in different positions in space. Therefore, they are not equal angles but congruent angles α≅β.

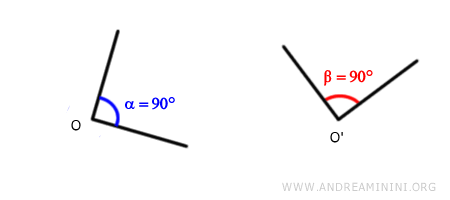
This means that while all equal angles are congruent, not all congruent angles are equal.

Note: Congruent angles correspond to an isometry because they can be superimposed after a rigid motion.

Other Methods for Comparing Angles

There are other methods to compare two angles in geometry:

• Direct Measurement
  Align the center of the protractor with the vertex of the angle (O) and the baseline of the protractor with one side of the angle. This allows you to directly read the measure of the angle's size on the protractor's arc. For example, angle α measures 60°.
  
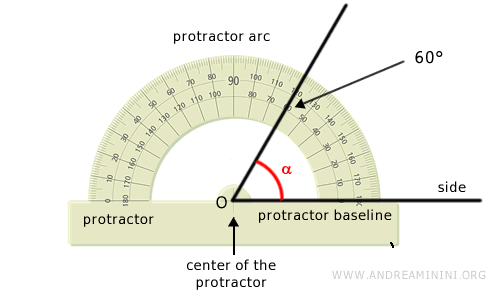
  Repeat the same operation for another angle, β. This way, you can compare the sizes of angles α and β based on their direct measurements in degrees or radians.
• Mathematical Calculations
  If you know the vectors that form the sides of the angles, you can use trigonometric formulas to calculate the angle's measure. For example, the angle between two vectors can be calculated using the dot product. Once the measurements are calculated, you can compare them to determine if the two angles are congruent or not.

In both cases, you can determine if two angles are congruent or if one is smaller or larger than the other.

And so on.