Congruence in Geometry
Two geometric figures are called congruent if they can be perfectly overlapped point by point through a rigid motion.
A rigid motion involves moving the figure without distortion through translation, rotation, and/or reflection.
Thus, two congruent figures have the same shape and size but occupy different positions in space.
To denote congruence, the "approximately equal" symbol, an equal sign with a tilde on top, is used: ≅
$$ A ≅ B $$
The concept of congruence is fundamental for identifying and comparing geometric figures.
Note: The concept of congruence is introduced within the context of Euclidean geometry. It is based on rigid transformations, or isometries, such as translations, rotations, and reflections. These transformations change the position of a figure in space but not its shape or size. Therefore, if one figure can be mapped onto another through a series of isometries, the two figures are congruent.
A Practical Example
Consider two copies of the same triangle,
One copy is upside down compared to the other.
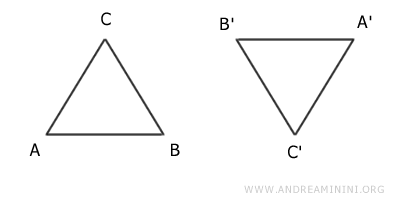
These two triangles are not identical because, although they have the same shape and size, they do not occupy the same space.
The two triangles are congruent because they have the same shape and size and can be overlapped after a rotation and a translation.
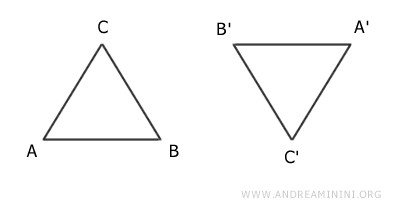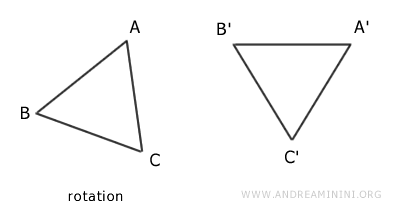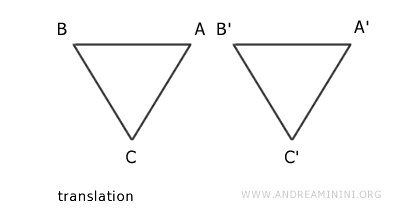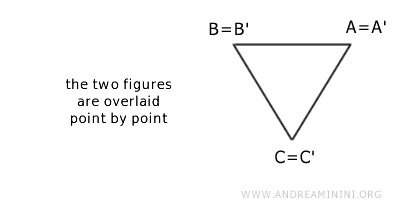
Once overlapped, the two geometric figures become identical.
Other Examples of Congruence
Specifically, in plane geometry:
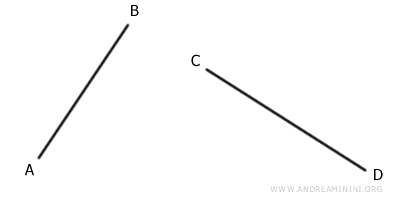
- Two segments are congruent if they have the same length. For example, AB≅CD
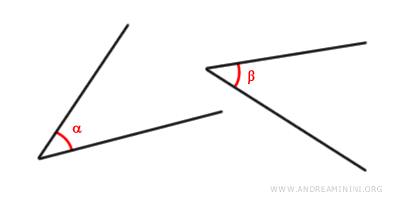
- Two angles are congruent if they have the same measure. For example, α≅β
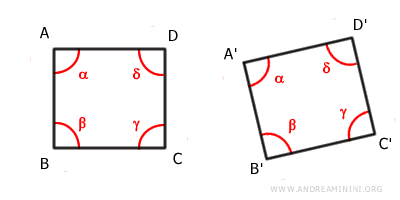
- Two polygons are congruent if their corresponding sides and angles are congruent.
Note: The congruence of segments leads to some important postulates in geometry:
- All lines are congruent to each other.
- All rays are congruent to each other.
- All half-planes are congruent to each other.
In other words, to establish the congruence between two geometric figures, certain criteria must be met.
For example, two triangles are congruent if they meet one of the following congruence criteria:
- SSS Criterion
Two triangles are congruent if all three sides are congruent, i.e., of the same length. - SAS Criterion
Two triangles are congruent if they have two sides and the included angle congruent. - ASA Criterion
Two triangles are congruent if they have two angles and the included side congruent.
Note: These congruence criteria are specific to triangles. If two triangles meet one of the above congruence criteria, they will also meet the others. Therefore, it is sufficient to verify just one criterion to establish the congruence of triangles.
What is the Difference Between Congruence and Equality?
The terms "congruence" and "equality" are often used interchangeably, but in geometry and mathematics, they have distinct meanings.
Two figures are equal if they coincide point by point without any rigid motion.
Thus, two equal geometric figures occupy exactly the same space, having the same shape, size, and position.
To denote equality in geometry, the mathematical equal sign "=" is used.
$$ A = B $$
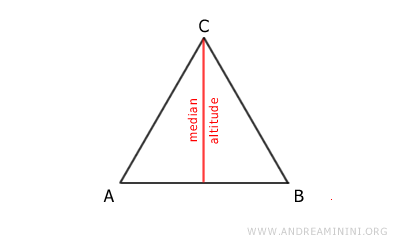
For example, the height and the median of an isosceles triangle are equal because they coincide point by point.
Congruence, on the other hand, requires that two figures can be overlapped point by point after a rigid motion.
Therefore, two congruent figures have the same shape and size but different positions, occupying different spaces.
To indicate congruence in geometry, the "approximately equal" symbol, an equal sign with a tilde on top, is used: ≅
$$ A ≅ B $$
For example, the legs AB and BC of an isosceles triangle are congruent because they can be overlapped after a rotation and translation.
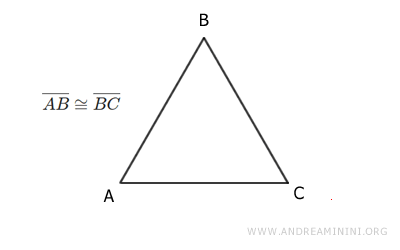
In conclusion, congruence is a more flexible concept than equality, specific to geometry, allowing figures of identical shape and size to have different positions.
Difference Between Congruence and Similarity
Congruence is also distinct from similarity.
In similarity, geometric figures have the same shape but different sizes.
For example, these two triangles are not congruent because they are not superimposable.
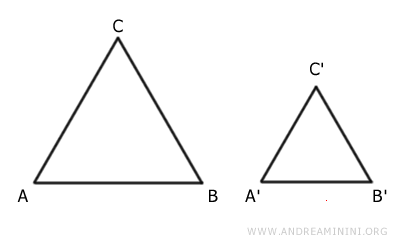
However, the two triangles are similar because they both have the same shape, being isosceles triangles, but different sizes.
The first isosceles triangle has longer sides compared to the second.
Properties of Congruence
It is important to note that congruence is an equivalence relation, meaning it satisfies the properties of reflexivity, symmetry, and transitivity:
- Reflexivity
Every figure is congruent to itself. - Symmetry
If figure A is congruent to figure B, then figure B is congruent to figure A. - Transitivity
If figure A is congruent to figure B and figure B is congruent to figure C, then figure A is congruent to figure C.
And so on.
