Analytic Geometry
Analytic geometry, also known as Cartesian geometry, is a branch of mathematics that uses algebraic techniques to represent and solve geometric problems.
In essence, analytic geometry establishes a connection between geometric figures and algebraic expressions.
How does it differ from Euclidean geometry?
Euclidean geometry is built on axioms and abstract geometric constructions, such as Euclid’s postulates.
In contrast, analytic geometry uses coordinates (x;y) or (x;y;z) along with algebra to represent geometric figures (e.g., points, lines, curves, planes, solids) and to solve geometric problems within the plane or in space.
The key concepts in analytic geometry include:
- Equations
Geometric shapes are represented by equations. For example, a straight line in the plane can be expressed as a linear equation with two variables $ ax+by+c=0 $, while a circle can be described by a quadratic equation $ x^2+y^2=r^2 $, where r is the radius. More complex equations can represent curves (such as parabolas, hyperbolas, and ellipses) or surfaces in space. - Coordinate System
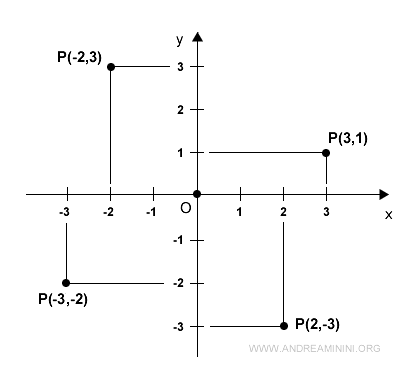
The most common system is the Cartesian coordinate system, or the "Cartesian plane," which uses two or three perpendicular axes to define the position of a point in the plane (2D) or in space (3D). Each point is identified by a pair (or triplet) of numbers called coordinates (x;y) or (x;y;z) that specify its location along the axes.
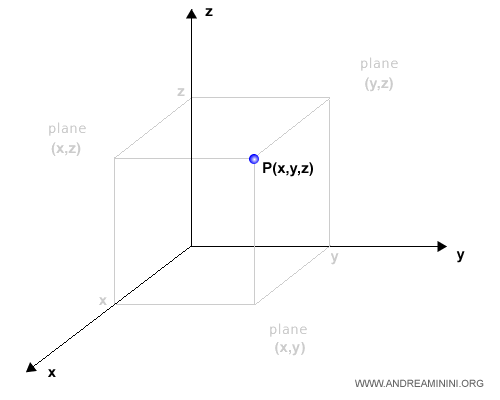
In three-dimensional space, the coordinates of each point consist of a triplet of numbers (x;y;z), corresponding to its position along the three axes.
One of the main objectives of analytic geometry is to determine the points where curves (or surfaces) intersect, which translates into solving systems of equations.
Analytic geometry also enables the calculation of the distance between two points or the angle between two lines using the coordinates of the points and the equations of the lines.
The Origin and History of Analytic Geometry. The introduction of analytic geometry in the 17th century by René Descartes (known in Italian as "Cartesio") and Pierre de Fermat marked a major milestone in mathematics, allowing for an unprecedented integration of algebra and geometry. This is why analytic geometry is also referred to as "Cartesian geometry." This approach paved the way for significant developments in various fields of mathematics and physics, including differential and integral calculus, classical mechanics, and relativity.
A Practical Example
Let's find the point of intersection between two lines on the Cartesian plane.
The lines are given by the following equations:
$$ L_1: y = 2x + 1 $$
$$ L_2: y = -x + 5 $$
To find the intersection point of the two lines, we need to determine the values of \(x\) and \(y\) that satisfy both equations simultaneously.
This involves solving the system of linear equations formed by the two line equations.
We set up the system of equations and solve for \(x\) and \(y\):
$$ \begin{cases} y = 2x + 1 \\ y = -x + 5 \end{cases} $$
$$ \begin{cases} -x + 5 = 2x + 1 \\ y = -x + 5 \end{cases} $$
$$ \begin{cases} -x - 2x = -5 + 1 \\ y = -x + 5 \end{cases} $$
$$ \begin{cases} -3x = -4 \\ y = -x + 5 \end{cases} $$
$$ \begin{cases} x = \frac{4}{3} \\ y = -x + 5 \end{cases} $$
Substituting \(x = \frac{4}{3} \) into the other equation to find \(y\):
$$ \begin{cases} x = \frac{4}{3} \\ y = -( \frac{4}{3} ) + 5 \end{cases} $$
$$ \begin{cases} x = \frac{4}{3} \\ y = \frac{-4 + 15}{3} \end{cases} $$
$$ \begin{cases} x = \frac{4}{3} \\ y = \frac{11}{3} \end{cases} $$
$$ \begin{cases} x = 1.3333 \\ y = 3.6667 \end{cases} $$
Therefore, the intersection point of the two lines \(L_1\) and \(L_2\) is \(\left(1.3333, 3.6667 \right)\).
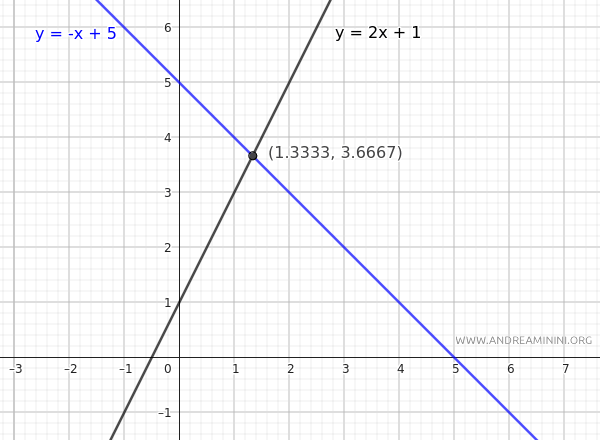
This example illustrates how analytic geometry can effectively solve geometric problems using algebra, without relying on a graphical representation.
And so on.
