Euclid's Postulates

In his seminal work "Elements," Euclid formulated five postulates that form the foundation of Euclidean geometry.

Euclid's five postulates are fundamental mathematical assertions assumed to be true without proof.

These postulates underpin plane geometry, which is commonly taught in schools.

Note: Rejecting even one of these Euclidean postulates leads to the development of a different type of geometry, known as non-Euclidean geometry.

These postulates are:

First Postulate

A straight line can be drawn connecting any two points.

This implies the conditions of existence and uniqueness: a unique straight line exists between any two distinct points.

Corollaries

From these axioms, several corollaries are derived:

• Infinite lines can pass through a single point.
• At least two points lie on any straight line.
• Through three non-collinear points, exactly one plane passes.
• Through three collinear points, exactly one straight line passes.
• Infinite planes can pass through a single straight line.

Second Postulate

A finite straight line can be extended indefinitely in a straight line.

Third Postulate

Given any point and any segment of length, a circle can be drawn with the point as its center and the segment as its radius.

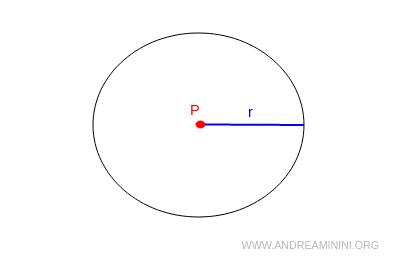
Fourth Postulate

All right angles are congruent, meaning they are equal in measure.

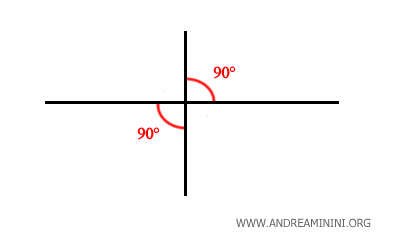
Fifth Postulate

If a straight line "r" intersects two other straight lines "s" and "t" such that the interior angles α and β on the same side are less than two right angles (α + β < 180°), then lines "s" and "t", if extended indefinitely, will meet at a point P.

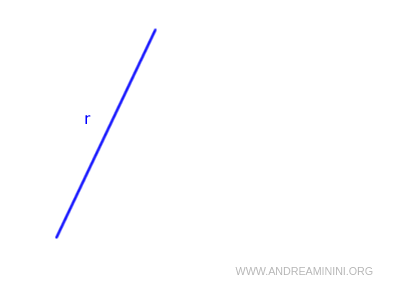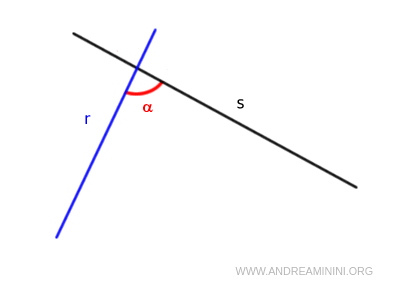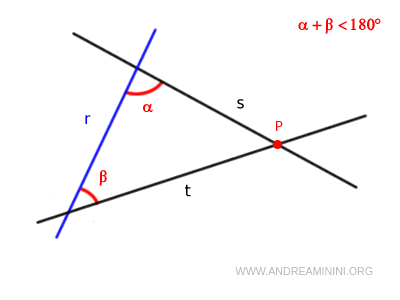
Euclid's fifth postulate is also known as the parallel postulate.

This is because if a straight line intersects two straight lines such that the sum of the interior angles is exactly 180°, then the two lines are parallel and will never intersect in the plane.

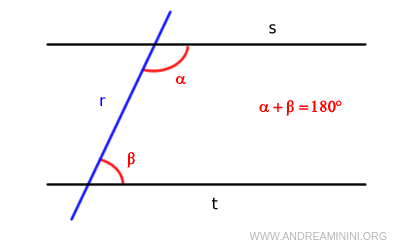
Over time, various formulations of this postulate have been proposed.

Note: Euclid's fifth postulate has been the subject of extensive debate and analysis over the centuries. For more than two thousand years, mathematicians attempted to derive this postulate from the other four but ultimately failed. In the 19th century, it was finally proven that this is not possible. Changing the fifth postulate results in a type of geometry entirely different from Euclidean geometry, known as non-Euclidean geometry. There are several types of non-Euclidean geometries, such as spherical geometry, hyperbolic geometry, and elliptic geometry.

And so on