Length

Length is the measurement of an object indicating its spatial extent. For example, the length of a line segment.

Length is one of the fundamental physical quantities because it is not defined by other physical quantities.

The unit of measurement for length in the International System of Units (SI) is the meter, along with its multiples (e.g., kilometer) and submultiples (e.g., centimeter, millimeter, etc.).

According to the current definition, a meter is the distance light travels in a vacuum in 1/299,792,458 of a second.

Note: The history of length measurement dates back to ancient civilizations due to its numerous practical applications (e.g., building construction, measuring trade routes, etc.). In ancient times, units of measurement were based on human body parts, such as the foot or the arm. For instance, the Egyptian cubit was the distance from the hand to the elbow. With technological and scientific advancements, these measurements were standardized to facilitate trade and scientific communication.

The Meaning of Length

Length is one of the most fundamental quantities for understanding and manipulating our world.

For example, a quick glance is often enough to tell if one stick is longer or shorter than another.

However, the apparent simplicity of "length" hides a deep complexity, as this term can have different meanings depending on the context, field of study, or technical or scientific discipline.

For instance, in Euclidean geometry, the length of a segment is simply the distance between its two endpoints.

Two segments are called congruent if they have the same length, meaning they can be superimposed, occupying the same points on a plane.

In these cases, the two congruent segments are said to belong to the same equivalence class.

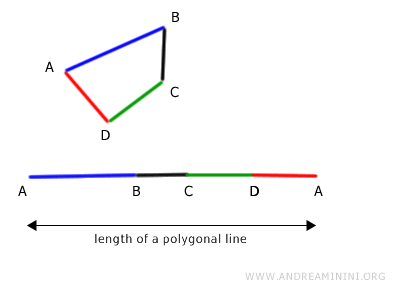
The length of a polygonal line, on the other hand, is the sum of the lengths of its component segments.

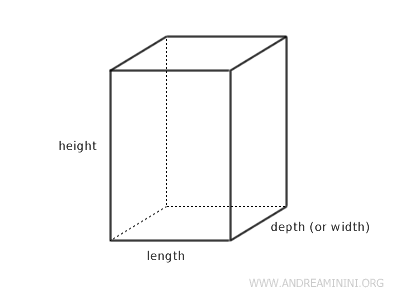
In solid geometry, length is one of the three dimensions, along with height and depth (or width), necessary to measure the size of an object.

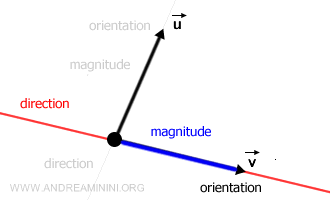
In linear algebra, length (or magnitude) is the modulus of a vector, synonymous with norm or absolute value.

A vector is typically represented by an arrow, and the modulus of the vector is the length of the arrow.

In physics, length is a fundamental physical quantity, measured in meters and denoted by [L] in dimensional analysis.

Thus, understanding the meaning of "length" requires attention to the context in which it is used.

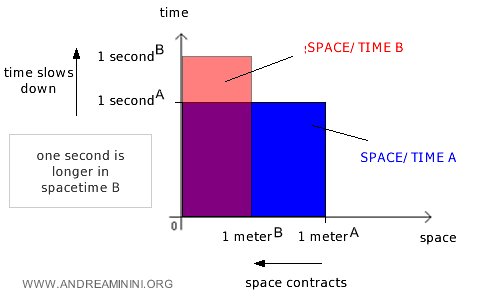
Note: In the context of Einstein's theory of special relativity, the issue becomes even more complex, as length takes on a new dimension, losing its meaning as an absolute measure and becoming a relative measure. For example, the length of a moving object is shorter than that measured by an observer at rest, a phenomenon known as length contraction. This effect occurs at speeds close to the speed of light.

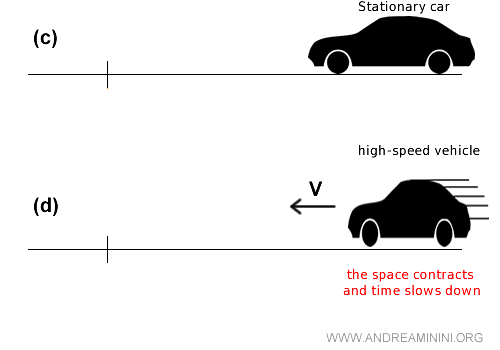
Additionally, in Einstein's general theory, space and time are seen as interdependent quantities rather than separate physical entities. Spacetime becomes a unified fabric that defines the structure of the universe. In this context, events are no longer localized in isolated points of space and discrete instants of time but rather in spacetime coordinates that highlight the inseparable interaction between space and time.

Measuring Length

In length measurement, precision and accuracy are crucial.

Tools for measuring length range from simple graduated rulers to sophisticated instruments like lasers and GPS devices.

In laboratories, lengths can be measured with extreme precision using interferometers.

Operations with Length

In Euclidean geometry, the properties of mathematical operations also apply to operations with lengths.

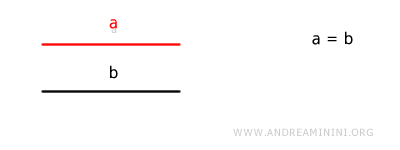
The length of a segment is usually indicated by a lowercase letter (e.g., a, b, c, ...).

For instance, segment congruence corresponds to the equality of two lengths (a=b).

$$ a = b $$

Comparing two non-congruent segments can determine if one is longer or shorter than the other (a<b or a>b).

$$ a < b $$

The sum of two segments is equal to the length of a segment obtained by concatenating their endpoints.

$$ a + b = c $$

The sum of two segments satisfies the following properties:

• Commutative: $$ a+b = b+a $$
• Associative: $$ (a+b)+c = a+(b+c) $$
• Existence of the neutral element: $$ a+0 = 0+a = a $$

And so on.