Calculating the Distance Between a Point and a Line Using Vectors

The shortest distance from a point P to a line is the length of the perpendicular segment PH, where P(x₀; y₀) is the given point and H is the point of intersection on the line.

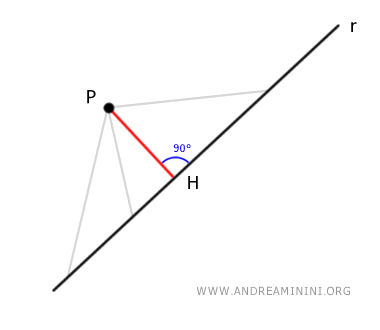
To calculate the length of segment PH, we use the following formula: $$ D(P(x_0,y_0),r) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$

A Practical Example

On the Cartesian plane, consider the line r

$$ 2x + 4y -6 = 0 $$

and a point A

$$ A \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$

Let's plot the line and the point on the Cartesian plane:

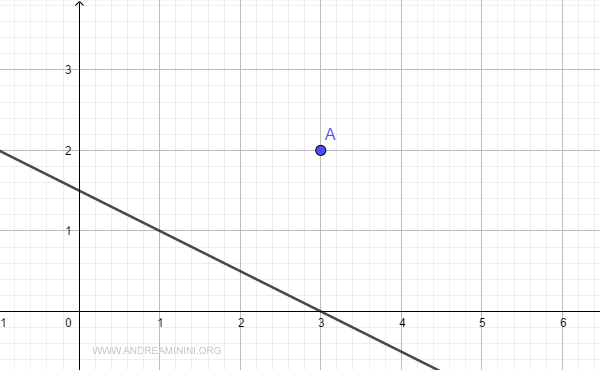
What is the shortest distance between the point and the line?

To determine the distance from point A to the line r, we use the formula:

$$ D(A(x_0,y_0),r) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$

Substituting the coordinates of point A:

$$ D(A(3,2),r) = \frac{|a(3)+b(2)+c|}{\sqrt{a^2+b^2}} $$

And the coefficients of the line:

$$ D(A(3,2),r) = \frac{|2 \cdot (3)+4 \cdot (2)-6|}{\sqrt{2^2+4^2}} = \frac{|6+8-6|}{\sqrt{4+16}} = \frac{8}{\sqrt{20}} = 1.78 $$

Therefore, the shortest distance between point A and the line is 1.78.

What is the closest point on the line to the point?

Knowing the shortest distance between point A and the line,

we now want to find the closest point on the line to point A.

This closest point lies on a line perpendicular to r that passes through point A.

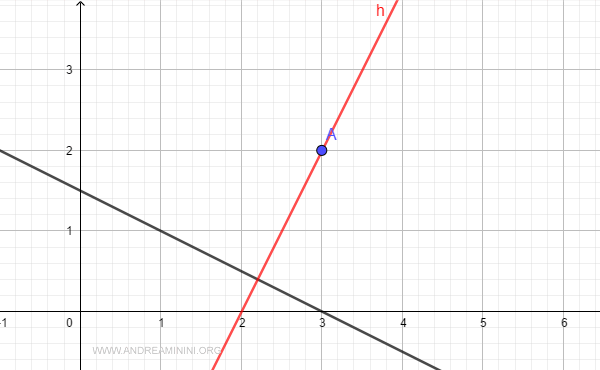
The vector equation of the perpendicular line r' is:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

Note: The coordinates (3,2) are point A, and the vector (2,4) is the normal vector, which is perpendicular to the direction vector of the line.

Converting the vector equation to parametric form:

$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \end{cases} $$

The point on the line closest to point A must satisfy this equation.

We add the equation of line r as an additional condition:

$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \\ 2x + 4y -6 = 0 \end{cases} $$

Solving the system for t:

$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \\ 2(3+2t) + 4(2+4t) -6 = 0 \end{cases} $$

$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \\ 6+4t + 8+16t -6 = 0 \end{cases} $$

$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \\ 8+20t = 0 \end{cases} $$

$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \\ 8+20t = \frac{-8}{20}= \frac{-2}{5} \end{cases} $$

We have found the parameter t for the perpendicular line r'.

Now, to find the coordinates of point H on the line closest to point A, we substitute the value of t into the parametric equations:

$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \end{cases} $$

$$ \begin{cases} x = 3 + 2 \cdot \frac{-2}{5} \\ y = 2 + 4 \cdot \frac{-2}{5} \end{cases} $$

$$ \begin{cases} x = \frac{15-4}{5} \\ y = \frac{10-8}{5} \end{cases} $$

$$ \begin{cases} x = \frac{11}{5} = 2.2 \\ y = \frac{2}{5} = 0.4 \end{cases} $$

Thus, we have found the coordinates of point H on the line.

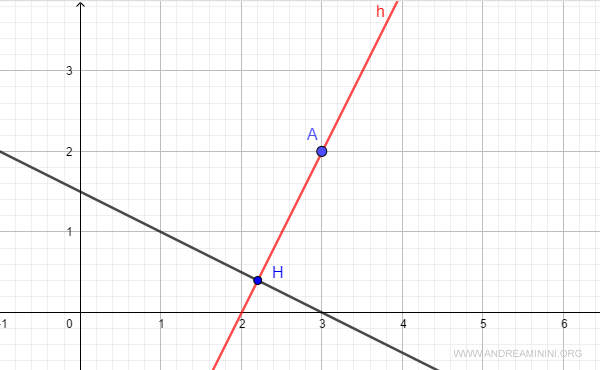
Note: To verify, we can calculate the distance between the two points AH. If everything is correct, the distance should match the distance between point A and line r. $$ || A-H || = || \begin{pmatrix} 3 - \frac{11}{5} \\ 2 - \frac{2}{5} \end{pmatrix} || = || \begin{pmatrix} \frac{4}{5} \\ \frac{8}{5} \end{pmatrix} || = $$ $$ || A-H || = \sqrt{(\frac{4}{5})^2+(\frac{8}{5})^2} = \sqrt{(\frac{16}{25})+(\frac{64}{25})} = \sqrt{\frac{16}{5}} = 1.78 $$ Perfect, it matches.

And that's it!