Topology

Topology is a branch of mathematics focused on properties of spaces that are preserved under continuous transformations like stretching, bending, and twisting. Examples of such properties include connectivity, compactness, and the number of holes an object has.

In simpler terms, topology deals with the arrangement and connectivity of spaces rather than precise measurements like distance or size.

In topology, traditional metrics like distance and angles are irrelevant; instead, the focus is on the qualitative nature of shapes and their potential transformations.

The foundational concept in topology is the topological space, and the key transformations are known as homeomorphisms.

Often described as "rubber-sheet geometry," topology views objects as if they were made of elastic that can be stretched or compressed, but not torn or glued. It forms a crucial part of modern mathematics.

History

Topology's development began in the 18th century.

Its origins trace back to Leonhard Euler's Seven Bridges of Königsberg problem, which introduced essential concepts of connectivity and network theory.

This problem sparked fundamental questions about the properties of spaces, establishing the groundwork for the field of topology.

The Seven Bridges problem: On a river island, there are seven bridges. Given any starting point, what route allows one to cross each bridge exactly once? Crucially, you cannot cross the same bridge more than once.

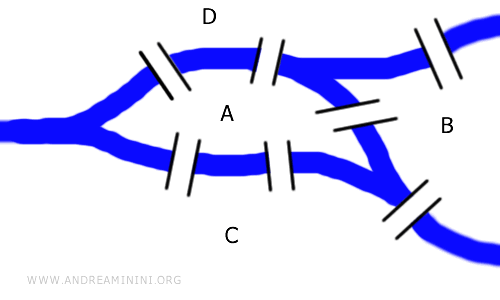
This challenge doesn’t require knowledge of distances or bridge lengths; it’s fundamentally a topological issue that can also be represented using graphs. The graph shown here is topologically equivalent to the original bridge layout.

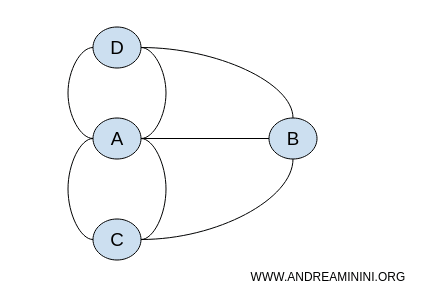
The specific positions of the nodes in the graph do not matter. What is important are the connections between the nodes. Thus, the problem could be represented with an infinite number of different but topologically equivalent graphs.

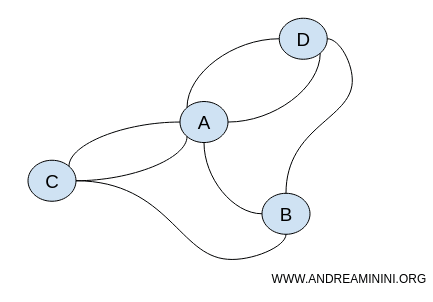
Both graphs maintain the same topological properties, such as continuity and connections.

Euler realized that the Seven Bridges of Königsberg problem, while geometric, did not hinge on measuring sizes.

He demonstrated that the challenge was fundamentally about position and showed that it was unsolvable, giving rise to the concept of "geometry of position."

Throughout the 19th century, mathematicians like Carl Friedrich Gauss, August Ferdinand Möbius, Johann Listing, Bernhard Riemann, and Felix Klein explored the properties of shapes and surfaces, further developing our understanding of topological properties.

Note: Johann Listing first coined the term "topology" in 1847, though it only gained widespread acceptance in the scientific community decades later.

In the 19th century, the geometry of position found practical applications in fields like electrical network analysis by Gustav Kirchhoff.

Subsequently, Henri Poincaré, in the late 19th and early 20th centuries, made significant contributions to geometry of position through his work in algebraic topology.

In the 20th century, topology branched into specialized subfields like algebraic topology and general topology, with significant contributions from mathematicians such as Felix Hausdorff, Cantor, and Brouwer, particularly in the realm of abstract mathematics.

Today, topology has become an essential field of mathematics focused on the study of properties that remain unchanged under continuous transformations.

Topology now encompasses several sub-disciplines, each focusing on different aspects of topological spaces, including algebraic topology, differential topology, general topology, and geometric topology.

Overall, topology can be viewed from a broader perspective as the general study of shapes and, theoretically, as an abstract mathematical discipline.

Despite its abstract nature, topological concepts are applicable to a variety of real-world problems in diverse fields such as economics, engineering, and science.

Topological Spaces

A topological space is a set X equipped with a structure T known as a "topology," which provides a framework for understanding abstract concepts like continuity, proximity, and limits in a broader and more general sense than traditional geometry or mathematical analysis.

$$ (X,T) $$

Example: A classic example of a topological space is the real number line \( \mathbb{R} \) with its standard topology, where a set is open if it contains an interval around every point. This setup facilitates the exploration of concepts like continuity and limits from a topological perspective.

Homeomorphisms

A homeomorphism is a bijective, continuous transformation between two topological spaces, whose inverse is also continuous, thus preserving fundamental topological properties.

Two spaces are considered essentially the same in topology if a homeomorphism exists between them.

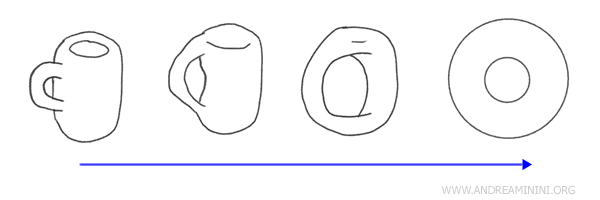
Example: Transforming a coffee cup into a donut is a classic example of a homeomorphism. Both objects have a single hole and can be morphed into each other through continuous deformations without cutting or gluing, thus maintaining their essential topological characteristics.

Geometry versus Topology

While geometry and topology are distinct fields, they are interrelated, each focusing on different aspects of mathematical spaces.

• Geometry deals with properties related to distances, angles, and measurements, focusing on concrete figures and their spatial relationships. An example is the rotation of a figure, a geometric transformation that preserves distances.
  

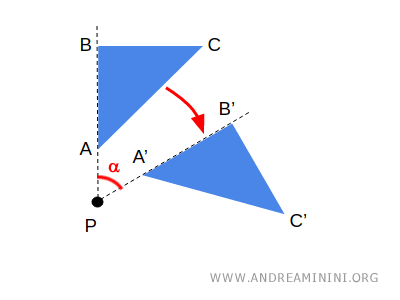
  Euclidean geometry is the most familiar form, but non-Euclidean geometries explore the implications of relaxing or negating Euclid’s fifth postulate (the parallel postulate).

• Topology focuses on properties that persist despite the space undergoing continuous transformations like stretching or compressing, without tearing or gluing. It concerns itself with qualitative aspects like continuity, connectivity, and the inherent flexibility of shapes. For instance, morphing a cube into a sphere maintains the connectivity among points and the overall continuity, characteristic of a topological transformation.
  

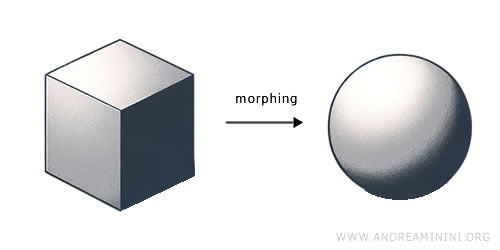
  Example: A cube made of clay can be reshaped into a sphere by compression, maintaining its continuity and connectivity without adding or removing material. This illustrates a homeomorphism, a fundamental type of topological transformation.
  

Despite their differences, the fields of topology and geometry are closely linked, with topology often considered a generalization of geometry.

Topology broadens the scope of investigation to include more abstract properties of spaces, unlike the more rigid focus of geometry.

Branches of Topology

Topology's applications span various areas of mathematics and science, each branch focusing on unique aspects of topological spaces.

• Topology in Geometry: Here, the focus is on the study of properties that are preserved through transformations like stretching, contracting, and folding, without tearing or gluing. This branch, known as geometric topology, looks at properties like continuity, connectivity, compactness, and boundaries without regard to distance.
• General Topology ( or Point-Set Topology): This branch studies topological spaces in a broad and abstract way, focusing on properties like open and closed sets, continuity, compactness, and connectivity, as well as on metric spaces and function spaces.
• Algebraic Topology: Algebraic topology uses algebraic tools to study topological spaces, linking algebraic structures to these spaces to understand their properties better.
• Differential Topology: This branch uses differential calculus to explore the properties and structures of topological spaces, particularly those resembling Euclidean space locally, allowing the definition of concepts like tangency and differentiability.
• Applied Topology: Applied topology refers to the use of topological methods in practical applications outside of pure mathematics, such as in data analysis, network science, engineering, and computational biology.

Each branch of topology has its own focus, methodologies, and applications, reflecting the versatility and broad applicability of topological concepts.