Simply Connected Spaces in Topology

A topological space is simply connected if every closed path within the space can be continuously transformed into a single point.

Put simply, a space is simply connected if any loop can be contracted to a point without leaving the space.

This indicates that the space is a cohesive "piece" (connected space) without any internal "holes."

Note: It follows that a simply connected space is also a connected space. However, the reverse is not necessarily true: not all connected spaces are simply connected.

A Practical Example

Take a sphere, for example, which is a simply connected topological space because any closed curve within it can be collapsed into a single point.

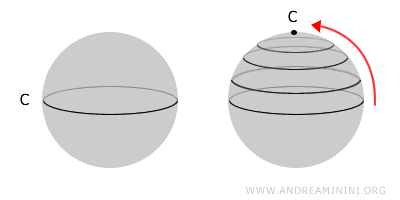
In contrast, a torus, or "doughnut," is not simply connected due to its central hole, which prevents some loops from being collapsed into a point.

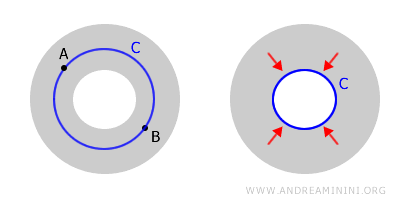
This also shows that being connected doesn't automatically imply simple connectivity.

The "doughnut" is a connected space because any two points A and B can be joined by a path that stays within the space.

However, the "doughnut" is not simply connected because not all its closed curves can be contracted to points.

In these instances, where a space is connected but not simply connected, it is known as a multiply connected space. Examples include the annular region or the toroidal space.

Thus, simple connectivity is a stronger condition than arc connectivity.

And so on.