Connectedness in Topology

In topology, a space is connected if it cannot be expressed as the union of two disjoint open sets. In simple terms, connectedness captures the idea that any two points in the space can be linked by a path that remains entirely within the space.

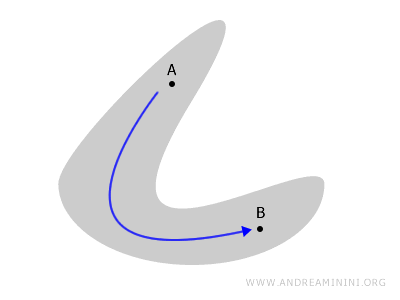
Connectedness describes how different parts of a topological space are either joined together or separated from one another.

It is a topological property because it is defined in terms of open sets.

This concept is one of the cornerstones of topology, closely related to the idea of continuity.

Connectedness plays a central role in many areas of mathematics, as it reveals essential aspects of a space’s structure and the relationships among its components. It is particularly useful for classifying and analyzing topological spaces.

A Practical Example

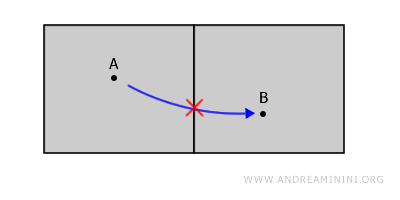
A figure in the plane or a solid in space is said to be connected if any two points A and B within it can be joined by a continuous path that never leaves the figure.

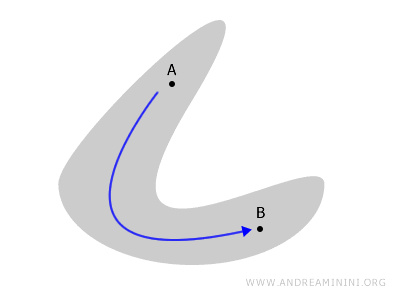
Conversely, if the space consists of separate parts, it is disconnected.

In the example below, the region is divided into two disjoint subsets. Any path connecting A and B would necessarily leave the space.

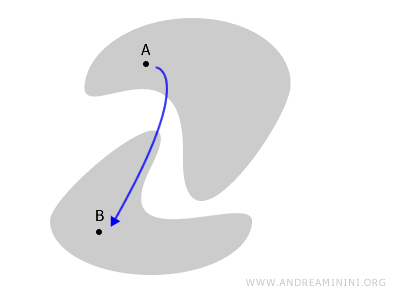
Let us explore this idea further with another simple illustration.

When is a Space Disconnected?

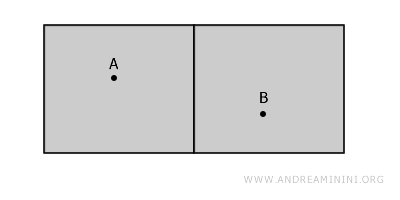
The simplest way to picture a disconnected space is to imagine two separate rooms in the same building, divided by a wall. Each room represents an open set that does not include the wall itself, and the two are disjoint.

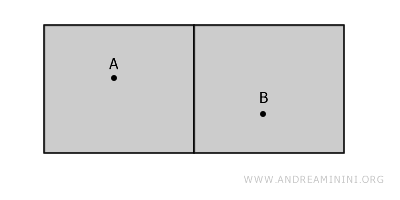
Although the rooms appear close, they are not connected, since any path from point A to B would have to pass through the wall, which lies outside the defined space.

In summary, boundaries are not part of open sets, and this is crucial when reasoning about connectedness.

Local Connectedness

A space is locally connected if every point has a connected neighborhood. In other words, each open set around a point contains a smaller connected open subset that includes the point.

Consider again the case of two disjoint rooms in a building.

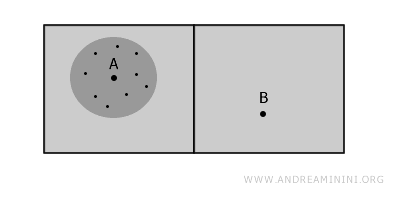
The overall space is disconnected because there is no continuous path linking A and B without crossing the wall. However, around point A there exists a smaller region where all points are mutually connected, showing that the space is locally connected at A.

The same reasoning applies to point B, which also has a connected neighborhood.

Types of Connectedness

Several forms of connectedness are studied in topology, but the most common are the following:

• Topological connectedness
  A topological space \( X \) is connected if it cannot be separated into two non-empty, disjoint open subsets whose union equals the entire space. In other words, the space cannot be “split” into two independent regions.

  Example. The interval (-1, 1) is connected, whereas the set (-1, 0) ∪ (0, 1) is not, since it can be written as the union of two disjoint non-empty open sets, (-1, 0) and (0, 1). These two sets form a separation of the space.

• Path connectedness (arc connectedness)
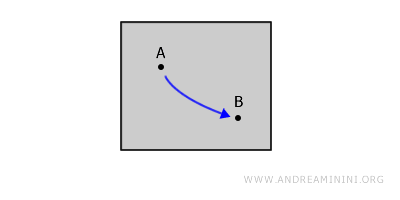
  A topological space is path connected if, for any two points A and B, there exists a continuous path within the space joining them. Every path-connected space is connected, though the converse does not always hold.

  For example, consider a closed region on a plane. For any two interior points A and B, you can draw a continuous curve between them without lifting your pen or leaving the region.
  
  Arc connectedness is a stronger condition: the connecting path must be one-to-one, meaning it does not cross or retrace itself.

• Simple connectedness
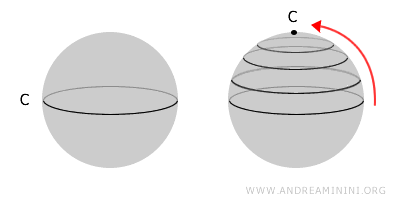
  A space is simply connected if every closed loop within it can be continuously contracted to a point. This means the space has no internal holes. Every simply connected space is connected, but not every connected space is simply connected. Formally, in a simply connected space, every loop is homotopic to a point.

  For example, a sphere is simply connected because any loop on its surface can be shrunk to a single point. In contrast, a torus (doughnut shape) is not simply connected, since loops encircling its hole cannot be contracted to a point.
  
  
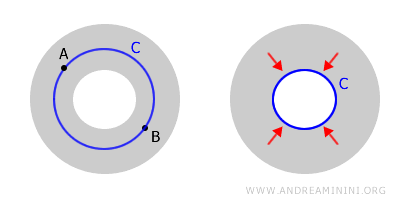
  A space that is connected but not simply connected is called multiply connected. An annulus is a typical example of such a space.

Notes

Some useful remarks:

• In the set of real numbers, the only connected subsets are intervals.