Limit Points in Topology

A point \(x\) in a topological space \(X\) is a limit point of a subset \(A \subseteq X\) if every neighborhood of \(x\) intersects \(A\) at some point other than \(x\).

This means that in every neighborhood of \(x\), there is at least one point in \(A\) that is not \(x\) itself.

In other words, a point \(x\) is a limit point if the intersection of every neighborhood \(U\) of \(x\) with the subset \(A\) is non-empty.

$$ U \cap A \not = \emptyset $$

A limit point can be any point, not necessarily one that belongs to the set \(A\).

Generally, the concept of a limit point is intuitive in a real topological space \(\mathbb{R}\). On a line, a point \(x\) is a limit point of a subset \(A\) if any neighborhood of \(x\), meaning an interval \((x-\epsilon, x+\epsilon)\), contains points of \(A\) other than \(x\).

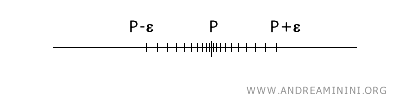
The topological definition of a limit point extends this concept to \(n\)-dimensional space \(\mathbb{R}^n\), where a point \(x\) is a limit point of \(A\) if every neighborhood of \(x\) intersects \(A\) at some point other than \(x\). This general definition is not always as intuitive as it is in one dimension.

Practical Examples

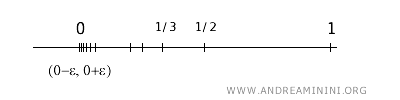
Consider the set \(A\) as a subset of \(\mathbb{R}\) with the standard topology.

$$ A = \left\{ \frac{1}{n} \mid n \in \mathbb{N}^+ \right\} $$

This set contains the points \( \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots \), that is, \(\{1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots \}\).

To determine if \(0\) is a limit point of \(A\), consider any open neighborhood \(U\) of \(0\).

Such a neighborhood \(U\) will contain an open interval \((a, b)\) with \(a < 0 < b\).

Since \(\frac{1}{n}\) tends to \(0\) as \(n\) approaches infinity, we can always find a point \(\frac{1}{n}\) within the interval \((a, b)\) for sufficiently large \(n\).

Therefore, every neighborhood of \(0\) intersects \(A\) at least at one point other than \(0\).

Thus, according to the definition, \(0\) is a limit point of the set \(A\).

Example 2

Consider the set \(B\) as a subset of \(\mathbb{R}\) with the standard topology.

$$ B = \left\{ n + \frac{1}{n} \mid n \in \mathbb{N}^+ \right\} $$

This set contains the points \( 1 + 1, 2 + \frac{1}{2}, 3 + \frac{1}{3}, \ldots \), that is, \(\{2, 2.5, 3.333\ldots, \ldots \}\).

Let's examine the point \(1\).

Any open neighborhood \(U\) of \(1\) will contain an open interval \((a, b)\) with \(a < 1 < b\).

However, all points of \(B\) are greater than \(1\), and for any point \(n + \frac{1}{n} \in B\), the interval \((a, b)\) will contain a point of \(B\) only if \(a < n + \frac{1}{n} < b\).

Since there are no points of \(B\) less than \(1\), it is impossible to find points of \(B\) in open intervals containing \(1\).

Therefore, \(1\) is not a limit point of the set \(B\).

Example 3

Consider the set \((0, 1] \) as a subset of \(\mathbb{R}\) with the standard topology.

We need to determine the limit points of \((0, 1]\).

According to the definition, a point \(x\) is a limit point of \((0, 1]\) if every neighborhood of \(x\) intersects \((0, 1]\) at some point other than \(x\).

1. Points within (0,1]
   For any \(x \in (0, 1]\), any neighborhood of \(x\) will be an open interval \((a, b)\) with \(a < x < b\). Since \(x\) is a point within the interval \((0, 1]\), every neighborhood of \(x\) will intersect \((0, 1)\) at some point other than \(x\). Therefore, every point \(x \in (0, 1]\) is a limit point of \((0, 1]\).
   
2. Boundary Points of (0,1]
   Let's examine the points \(0\) and \(1\).
   - Point \(0\): Any neighborhood of \(0\) will contain an open interval \((a, b)\) with \(a < 0 < b\). Even though \(0\) is not in \((0, 1]\), any such interval will contain infinitely many points of \((0, 1]\). For example, any very small positive real number will be in \((0, 1]\). Therefore, \(0\) is a limit point of \((0, 1]\).
   
   - Point \(1\): Any neighborhood of \(1\) will contain an open interval \((a, b)\) with \(a < 1 < b\). In this case, \(1\) belongs to \((0, 1]\) and is a limit point because any such interval will contain infinitely many points of \((0, 1]\). For example, any real number just below \(1\) will be in \((0, 1]\). Therefore, \(1\) is a limit point of \((0, 1]\).
   
3. Points outside [0, 1]
   For completeness, let's consider a generic point outside the interval and the limit points we have just found, that is, \(x \notin [0, 1]\). If \(x < 0\) or \(x > 1\), we can always find a neighborhood of \(x\) that is completely disjoint from \((0, 1]\).

   For example, if \(x < 0\), we can take an interval \((x - \epsilon, x + \epsilon)\) with \(\epsilon\) small enough so that it does not intersect \((0, 1]\). Similarly, if \(x > 1\), we can find an interval around \(x\) that does not intersect \((0, 1]\). Thus, no points outside \([0 , 1]\) are limit points of \((0, 1]\).

In conclusion, the limit points of the set \((0, 1)\) in the topological space \(\mathbb{R}\) with the standard topology are all the points in the closed interval \([0, 1]\).

Example 4

I need to determine the set of limit points of \( A = (0, 1] \) in the lower limit topology on \( \mathbb{R} \).

The lower limit topology on \( \mathbb{R} \) is generated by intervals of the form \([a, b)\) with \( a < b \). Therefore, the open sets in this topology are arbitrary unions of these intervals.

A point \( x \) is a limit point of a set \( A \) if every neighborhood of \( x \) contains at least one point of \( A \) other than \( x \).

Let’s examine the different points in the space:

• Points x ∈ (0, 1)
  Any neighborhood \([x, x + \epsilon)\) with \( x \) in (0,1) contains points of \( A \). Hence, \( x \) is an accumulation point of \( A \).
• Point x = 1
  Any neighborhood \([1 - \epsilon, 1)\) contains points of \( A \). Thus, \( 1 \) is also an accumulation point of \( A \).
• Point x = 0
  Any neighborhood \([0, 0 + \epsilon)\) with \(\epsilon > 0\) contains points of \( A \), so \( 0 \) is also a limit point of \( A \).
• Points x < 0  or  x > 1
  There is nothing to say here, as there are no neighborhoods \([x, x + \epsilon)\) that intersect \( A \). Therefore, these points are not accumulation points of \( A \).

In conclusion, the accumulation points of \( A = (0, 1] \) in the lower limit topology on \( \mathbb{R} \) are all the points in \([0, 1]\).

Thus, the set of limit points of \( A \) is \([0, 1]\).

Remarks

Some observations and notes about limit points:

• The closure of a set equals the union of the set and its limit points
  The closure of a subset \(A\) in a topological space \(X\) is the union of \(A\) with the set \(A' \) of its limit points: $$ \text{Cl}(A) = A \cup A' $$ In other words, the closure \(\text{Cl}(A)\) contains all the points in the set \(A\) and all its limit points.
• A sequence of points converges to an accumulation point
  If $ A $ is a subset of the topological space $ X = \mathbb{R} $ with the standard topology and $ x $ is an accumulation point of $ A $, then there exists a sequence of points $ x_i \in X $ that converges to $ x $. Note that the limit point does not necessarily belong to the subset $ A $.
• Uniqueness of the limit point
  In the standard topology, if a sequence of points converges to a limit point $ x $, then this point is unique. However, this is not always the case as it depends on the topology being used.

And so on.