Quotient Topology

Let $X$ be a topological space and $A$ a set that is not necessarily a subset of $X$. Suppose $p: X \rightarrow A$ is a surjective map. A subset $U$ of $A$ is open in $A$ if and only if $p^{-1}(U)$ is open in $X$.

In other words, a set $U$ in $A$ is open in the quotient topology on $A$ if and only if its preimage $p^{-1}(U)$, the set of points in $X$ that map to $U$ under $p$, is open in $X$.

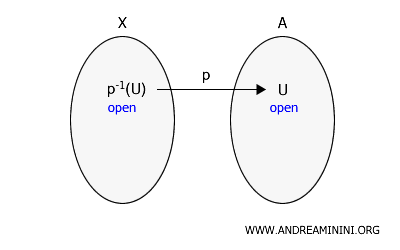
quotient topology

This concept is used to define a new topology on $A$, known as the quotient topology, which is derived from the topology on $X$ via the map $p$.

The set $A$ is called the quotient space, while $p$ is referred to as the quotient map.

The collection of open sets in $A$ is often described as the "quotient topology induced by $p$."

This means that in quotient topology, a set is considered open if its preimage in the original space is open.

It's important to clarify a common misconception:

The preimage of an open set in the quotient space $A$ is open in the original space $X$, but the reverse does not always hold.
The image of an open set in the original space $X$ is not necessarily open in the quotient space $A$, because the map $p: X \rightarrow A$ may distort it.

In summary, a quotient space is a topological space formed from another space by identifying, or "gluing," certain points together according to an equivalence relation.

Put simply, a quotient space is the result of "gluing" or grouping points in a space based on a specific rule, and then studying the topological properties of the resulting space.

So, why is the quotient topology useful? By constructing a quotient topology, we can study how the quotient space $A$, which may be more complex, behaves, using the information we have about $X$, the original space, which is often easier to work with.

Explanation
A Practical Example
Properties of the Quotient Topology

Explanation

The concept of "quotient topology" can be challenging, but I’ll try to break it down more simply.

The "quotient topology" is a way to transform a shape into a new form by gluing together some of its edges or sides.

For example, imagine you have a square piece of paper. If you glue two opposite sides together, you can form a cylinder.

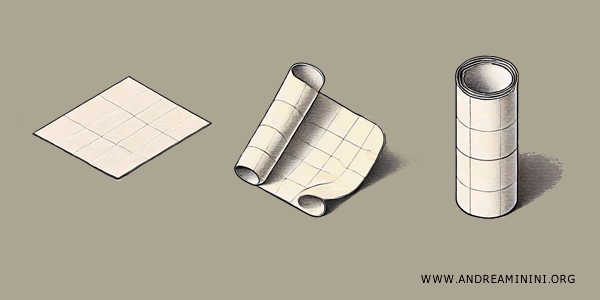
folding the paper onto itself

If you then glue the circular edges of the cylinder together, you get a doughnut or a torus.

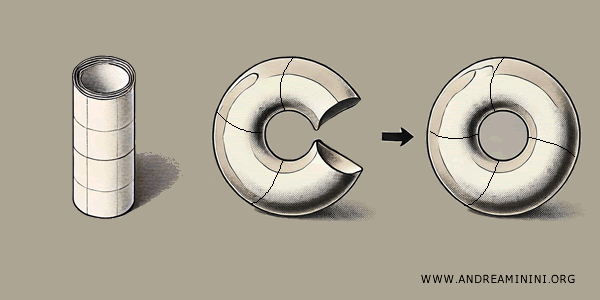
example of a torus

In this example, the square is first transformed into a cylinder and then into a torus (a doughnut shape) by gluing the opposite sides together.

Similarly, the quotient topology allows us to create new shapes or topological spaces from simpler ones by "gluing" certain parts together.

This concept is widely used in mathematics to study the properties of surfaces and spaces in a more abstract way.

A Practical Example

Consider the topological space $ X = [0, 1] $ with the usual topology, where open sets are open intervals or unions of open intervals.

In this space:

The set $ X $ and the empty set $ \emptyset $ are open by definition.
Every open interval $ (a,b) $ with $ 0 \leq a < b \leq 1 $ is open in $ X $.

You can think of the space $ X $ as a line segment with one end at $ 0 $ and the other at $ 1 $.

example of a segment [0,1]

Now, let's create a new quotient space by gluing together the points $ 0 $ and $ 1 $ of the interval $[0, 1]$. Essentially, we are "identifying" $ 0 $ and $ 1 $ as if they were the same point.

To do this, we define a map $ p: [0, 1] \rightarrow A $ as follows:

$$ p(x) = \begin{cases} p(0) & \text{if } x = 0 \text{ or } x = 1 \\ \\ x & \text{if } 0 < x < 1 \end{cases} $$

The new quotient set $ A $ that we obtain by identifying $ 0 $ and $ 1 $ can be visualized as a circle, where the points $ 0 $ and $ 1 $ have been "glued" together.

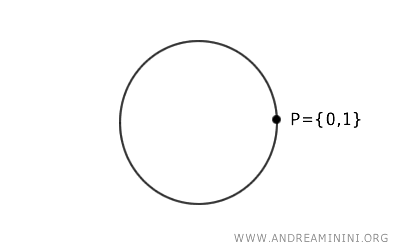
quotient topology

In other words, I've "curved" the line segment to join the ends 0 and 1 together.

In the new space $ A $, the point $ P = \{0, 1\} $ is the image of both the point $ 0 $ and the point $ 1 $ in $ X $ under the map $ p $.

Now, to define the topology on $ A $, we need to determine which sets in $ A $ will be considered open.

According to the definition of the quotient topology, a set $ U \subseteq A $ is open in $ A $ if its preimage $ p^{-1}(U) $ is an open set in $ [0, 1] $.

Let’s look at two cases:

Interval $ U = (a,b) $ that does not contain $ P $
Its preimage in $ X $ is the interval $ (a,b) $, which is open in $ X $. Therefore, $ U $ is open in $ A $.
Interval $ U = (a,b) $ that contains $ P = \{0,1\} $
The preimage in $ X $ is the union of two intervals $ [0,a) \cup (b,1] $, both of which are open in $ X $. Thus, $ U $ is open in $ A $.

In this way, we've created a new topological space $ A $, which is a circle, from a simpler space, the interval $ [0, 1] $.

This is a classic example of how the quotient topology can transform a simple space into a more complex one.

Example 2

In this example of quotient topology, I want to "wrap" the real line around a circle.

Consider the real line ($ \mathbb{R} $), which extends infinitely in both directions.

Now, I want to "wrap" the real line onto a circle by identifying each real number with its fractional part.

We do this with a map defined as $ p(x) = x \mod 1 $.

What does this mean? It’s straightforward: for any real number $ x $, we take only its decimal part (the part after the decimal point) and use that to represent a point on the circle.

For example, if $ x = 1.3 $, the map takes the decimal part, 0.3, and places it at a point on the circle. If $ x = 2.7 $, the decimal part is 0.7, so it corresponds to the same point on the circle as $ 0.7 $.
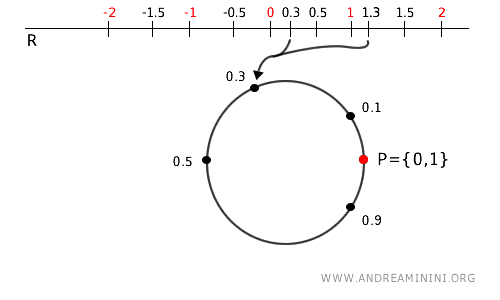
example

Each time $ x $ increases by an integer (for example, from 1.3 to 2.3 or 3.3), the point ends up at the same spot on the circle.

This is what I mean by "wrapping" the line onto the circle, where points 0 and 1 coincide.

Now, let’s look at a few intervals.

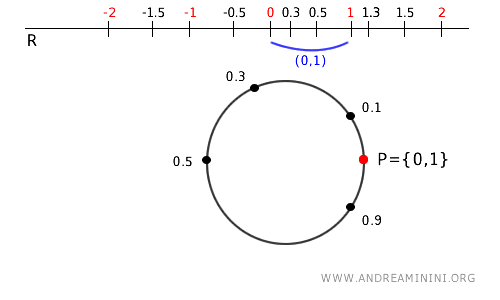
Interval (0,1) on $ \mathbb{R} $
The interval $ (0, 1) $ on $ \mathbb{R} $ wraps around an arc of the circle, but it doesn’t include the point 0 on the circle. We can say that the interval (0,1) is open in the quotient space (the circle) because its preimage (0,1) is open in the original space $ \mathbb{R} $.
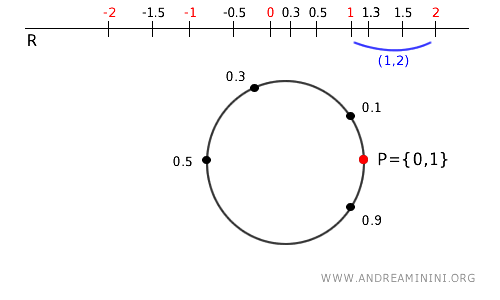
Interval (1,2) on $ \mathbb{R} $
The interval $ (1, 2) $ on $ \mathbb{R} $ also wraps around the same arc since 1 and 2 are both identified with 0 (i.e., $ 1 \mod 1 = 0 \mod 1 $). In other words, the interval (1,2) on $ \mathbb{R} $ maps once again to the interval (0,1) on the circle, which we already know is open in the quotient topology. So, this doesn’t give us any new information.
Interval (0,2) on $ \mathbb{R} $
The interval $ (0, 2) $ on the real line is an open interval. It stretches from 0 to 2, but what happens when we wrap it around the circle using the map $ p $? The interval $ (0, 2) $ covers the entire circle because it includes 1, wrapping around twice over the same arcs. So, the interval $ (0, 2) $ on the real line covers the entire circle. Even though $ (0, 2) $ is open on the real line, its image after wrapping is the whole circle, which in this case is both open and closed (clopen). Since a circle has no true boundary, the entire circle can be considered open and closed at the same time.

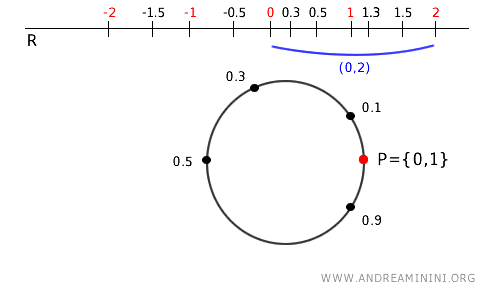
Note: This shows that an open set in the original space does not necessarily map to an open set in the quotient space.

In general, if we take an open set on the circle, its preimage on the real line will always be open.

This works because whenever we "unwrap" an open set from the circle to the real line, we get open intervals.

However, the reverse isn’t true—if we take an open set in the original space, its image won’t necessarily be open in the quotient space.

Moral of the story

We can’t always assume that an open set on the real line will have an open image on the circle, because the wrapping map can "compress" or "distort" the sets, altering their topological behavior.

Example 3

In this exercise, I aim to create a quotient topology by connecting the first ($ m $) and last ($ n $) numbers in a consecutive sequence of integers $ \{ m, m+1, ..., n \} $ from $ \mathbb{Z} $.

Consider a sequence of 7 consecutive integers from 1 to 7.

$$ I_7 = \{1, 2, 3, 4, 5, 6, 7\} $$

This is a digital interval because it consists of consecutive whole numbers.

Now, I link the first number (1) with the last number (7). It's akin to taking a straight line and joining its ends to form a loop or circle.

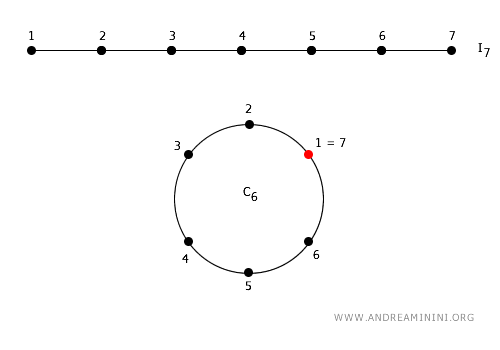
example of a digital circle

By doing this, I create a new topological structure called a digital circle $ C_6 $, which consists of 6 points.

Each point in this circle is adjacent to two other points.

This is an example of a quotient topology because we have generated a new topological space that differs from the original digital interval.

Note: The result is similar to the circle obtained by connecting the ends of a real interval (a, b). However, in this case, it is made up of integers, forming a finite set of points.

The digital circle also serves as an example of digital topology, as each point is connected to its neighbors.

Thus, it is a discrete space where concepts of digital topology, such as connectivity and the definition of digital open sets, can be applied.

Note: In digital topology, a set $ U $ is considered open if every point $ x \in U $ includes its neighboring points, depending on the type of connection chosen. Examples include 2-connection in a circle or ring (1D), 4-connection or 8-connection on a plane (2D), or 6-connection or 18-connection in space (3D).

It's crucial to emphasize that quotient topology and digital topology are distinct.

In other words, while the digital circle can be constructed as a quotient topology, it can also be classified as a digital topology. However, these two topologies should not be conflated.

Example 4

Consider the set of real numbers $ \mathbb{R} $ with the standard topology, and a quotient map $ p: \mathbb{R} \to \{a, b, c\} $ defined as follows:

$$ p(x) = \begin{cases} a \ \ if \ \ x < 0 \\ \\ b \ \ if \ \ x = 0 \\ \\ c \ \ if \ \ x > 0 \\ \\ \end{cases} $$

In essence, I’m collapsing the entire set of negative numbers into $ a $, the point $ 0 $ into $ b $, and the positive numbers into $ c $.

The quotient topology induced by this map depends on the preimages of the elements $ a $, $ b $, and $ c $.

The preimages are:

$ p^{-1}(a) = (-\infty, 0) $, which is an open set in $ \mathbb{R} $,
$ p^{-1}(b) = \{0\} $, which is **not** open in $ \mathbb{R} $,
$ p^{-1}(c) = (0, \infty) $, which is open in $ \mathbb{R} $.

Since, in the quotient topology, a set in $ \{a, b, c\} $ is open if its preimage under $ p $ is open in $ \mathbb{R} $, we can conclude that the following sets are open in the quotient topology:

The set $ \{a\} $ is open because its preimage $ (-\infty, 0) $ is open in $ \mathbb{R} $.
The set $ \{c\} $ is open because its preimage $ (0, \infty) $ is open in $ \mathbb{R} $.
The union $ \{a, c\} $ is open because its preimage $ (-\infty, 0) \cup (0, \infty) = \mathbb{R} \setminus \{0\} $ is open in $ \mathbb{R} $.

In the quotient topology, both the entire set and the empty set are open.

The entire set, i.e., the whole space {a,b,c}, is always open in any quotient topology because the preimage of {a,b,c} under the map p is the full set of R, which by definition is open in its standard topology.
The empty set ∅ is another fundamental example and is always open. The preimage of the empty set under p is still the empty set in R, which is, by definition, open in any topology.

However, the set $ \{b\} $ is not open in the quotient topology because its preimage $ \{0\} $ is not open in $ \mathbb{R} $.

In conclusion, the quotient topology on $ \{a, b, c\} $ has the sets $ \emptyset $, $ \{a,b,c \} $, $ \{a\} $, $ \{c\} $, and $ \{a, c\} $ as open sets, while $ \{b\} $ is not open since the point $ 0 $ on the real line is not an open set.

Essentially, $ b $ is a "singularity"—an isolated point that cannot be included in an open set.

Properties of the Quotient Topology

Here are some useful properties of the quotient topology to keep in mind:

The empty set and the quotient set are open in the quotient topology
Both the empty set and the entire quotient set are considered open in the quotient topology.
- Preimage of the empty set
  The preimage of the empty set $ p^{-1}(\emptyset) $ under the map $ p $ remains the empty set $ \emptyset $, which is open in $ X $. Thus, $ \emptyset $ is open in the quotient topology as well.
- Preimage of the entire set
  The preimage of a set $ A $ under $ p $ is the entire set $ X $, which is open in $ X $. Therefore, $ A $ is also open in the quotient topology.
Note: In other words, the empty set and the entire set are always open in any topology, so their images in the quotient topology will also be open. The image of the empty set under the map $ p: X \rightarrow A $ is still $ \emptyset $, while the image of the entire set $ X $ is the set $ A $.
Union of open sets in the quotient topology
If $ U_i $ is open in the quotient topology on $ A $, then its preimage under $ p $ is open in $ X $. Therefore, the union of open sets in $ A $ corresponds to a union of open sets in $ X $: $$
\left( \forall i, \ U_i \text{ is open in } A \right) \Rightarrow p^{-1}\left( \bigcup U_i \right) = \bigcup p^{-1}(U_i) \text{ is open in } X $$ Thus, any arbitrary union of open sets in the quotient topology remains open in $ A $.
Note: The union of open sets $ \bigcup U_i $ in the quotient topology on $ A $ is still an open set. This implies that the preimage of the union $ p^{-1}( \bigcup U_i ) $ is also open in $ X $. The preimage of a union is the union of the individual preimages, i.e., $ p^{-1}\left( \bigcup U_i \right) = \bigcup p^{-1}(U_i) $, and since each $ p^{-1}(U_i) $ is open in $ X $, the union of these preimages is open in $ X $. Consequently, since the preimage of $ \bigcup U_i $ is open in $ X $, this means that $ \bigcup U_i $ remains open in the quotient topology on $ A $. Therefore, the property of openness is preserved under the quotient map $ p $.
Intersection of open sets in the quotient topology
If the sets U_i are open in the quotient space, then the intersection of their preimages remains open in the original space X.
Note. Put simply, $ U_i $ are open sets in the quotient space $ A $. The quotient map $ p: X \to A $ has the key property that the preimage of an open set in the quotient remains open in $ X $. Hence, each preimage $ p^{-1}(U_i) $ is open in the original space $ X $. Since the finite intersection of open sets in $ X $ is also open, it follows that $ \bigcap p^{-1}(U_i) $ will be open in $ X $. In summary, if the sets are open in the quotient space, the intersection of their preimages will be open in the original space.

And so on.