Digital Topology

Digital topology refers to a topological structure defined on a discrete space, such as a grid of points (pixels in 2D, voxels in 3D), which represents the connection properties between points based on a specific adjacency relation.

In this framework, open sets are characterized by the connections between points, with the type of connection varying according to criteria such as 4-connectivity, 8-connectivity (in 2D), or 6-connectivity, 18-connectivity, and 26-connectivity (in 3D).

Digital topology is widely used in applications like image processing, digital graphics, and computer vision, as it adapts concepts from classical topology to a discrete environment.

Open Sets in Digital Topology

In digital topology, a set \(U\) is considered open if, for every point \(x \in U\), its adjacent points, as determined by the chosen type of connectivity, are also included in \(U\).

The idea of "adjacent" or "neighboring" points depends on the specific type of connection selected in the digital space. For example:

On a ring or circular grid, each point is adjacent to two other points, representing a 2-connectivity structure.

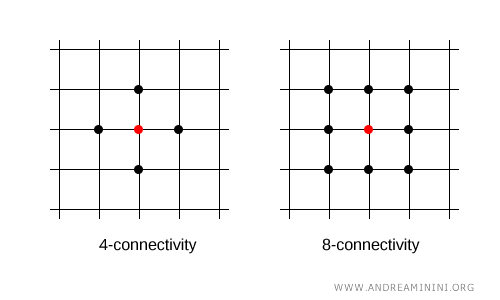
In the 2D plane, a point can be connected to four other points (4-connectivity) to the north, south, west, and east, or to all eight neighboring points (8-connectivity), including those on the diagonals.

In a three-dimensional digital space (3D), the connection of each point to its neighboring points, which belong to the digital space and are also part of \(U\), can be based on 6-connectivity, 18-connectivity, or 26-connectivity.

Example

Consider a set of points arranged in a digital circle (discrete space) with a 2-connectivity.

Each point in the set has two neighboring points directly to its left and right.

For instance, point 2 is adjacent to points 1 and 3.

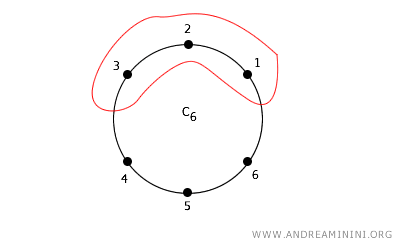
In this context, a set \(U\) is open in digital topology because all the neighbors of every point within \(U\) are also contained in \(U\).

This notion reflects the idea of continuity and connection between points, tailored to the discrete nature of digital spaces.

Difference Between Digital Topology and Discrete Topology

Digital topology is not the same as discrete topology, even though both involve discrete topological spaces. Key differences include:

• Discrete Topology
  A topology on a set \(X\) is called discrete if every possible subset of \(X\) is an open set.
• Digital Topology
  In contrast, digital topology is adapted to discrete sets where the definition of an open set depends on the connections between points.

So, what's the distinction?

In discrete topology, every subset is open. In digital topology, not every subset is necessarily open; only those sets that satisfy the specified connectivity criteria are considered open.

Therefore, digital topology is not a discrete topology because not all subsets are guaranteed to be open.

For instance, a set consisting of two isolated, unconnected pixels is not an open set in digital topology. However, the same set would be open in discrete topology.

In essence, digital topology is designed to capture the notion of connectivity between points in a digital space, while discrete topology overlooks any form of connection, treating each point as an independent entity.

Example

Consider the set of points \(\{1, 2, 3, 4\}\) arranged in a circular structure with digital topology based on 2-connectivity.

• The set \(\{1, 2\}\) is open in digital topology because points 1 and 2 are directly adjacent.
• The set \(\{1, 3\}\) is not open because points 1 and 3 are not directly connected.

If we were to consider the same set of points \(\{1, 2, 3, 4\}\) in discrete topology, both \(\{1, 2\}\) and \(\{1, 3\}\) would be regarded as open sets since, in this topology, every subset is open.

Note. In the same discrete metric space \(\{1, 2, 3, 4\}\), digital topology is more restrictive than discrete topology because it imposes a connectivity requirement for defining open sets.

And so forth.