Basis of Topology

The basis of topology refers to a collection B of open sets such that every open set in the topological space T can be represented as a union of sets from the basis B.

When you have a set X and a collection T of subsets of X that define a topology on X, the basis of the topology T is a collection B of sets, called basic elements, which satisfy the following conditions:

Every element x in the set X must belong to at least one set contained in B.
For any element x in set X that lies in the non-empty intersection B₁∩B₂ of a pair of sets belonging to B, there must be a set B₃ within the intersection that contains x. In other words, the element x is a basic element.

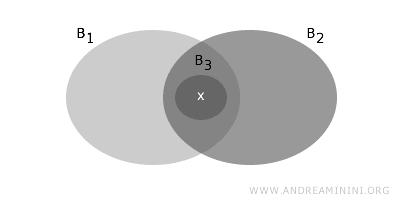
These conditions ensure that the collection of sets B forms a basis for the topology T.

Why is this important?

The basis of topology allows us to construct the topology T through the union of basic elements, without the need to enumerate every single set in the collection T.

Note. The property regarding the intersections of basic elements ensures that the topology satisfies fundamental axioms, including the condition that the intersection of two open sets is open.

A Practical Example
Countable Basis
Observations

A Practical Example

Let's consider the set X

$$ \{a, b, c \} $$

and the topology T

$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$

In this case, T represents all the open sets in X, and each element of T is an open set by definition.

A basis B for this topology could be as follows:

$$ B = \{ \{ a \} ,\{ b,c \} \} $$

This basis satisfies all necessary conditions since every element of X={a,b,c} is included in a subset of B and there are no intersections.

Note that every open set in T can be expressed as a union of sets in B.

For example, the set {a} is already in B, the set {b,c} is also in B, and the entire space X can be obtained by uniting {a} and {b,c}.

$$ \{ a \} \in B $$

$$ \{ b,c \} \in B $$

$$ \{ a,b,c \} = \{ a \} \cup \{ b,c \} $$

Note. In set theory, the empty set Ø is an improper subset of any set and is always included by definition. Thus, it is also present in B. $$ \emptyset \in B $$ Moreover, the empty set is an open set by definition in a topology.

This example illustrates the concept of an open set in a finite context.

In more complex or infinite contexts, the definition of a basis and its application can become more sophisticated, but the underlying idea remains the same: a basis provides the "building blocks" for all open sets in the topological space.

Another Approach

An alternative basis B for the topology on the set X={a,b,c} could be:

$$ B = \{ \{ a \} ,\{ b \}, \{ c \} \} $$

In this case, the basis consists of the singleton sets of elements of X.

This verifies that B indeed forms a basis for the topology T={ Ø,X,{a},{b,c}}

The empty set Ø is an open set by definition and does not require elements to be constructed. It's also an improper subset of any set and is always included.
The set {a} is already in B. $$ \{ a \} \in B $$
The set {b,c} can be obtained from the union of {b} and {c}, both present in B. $$ \{ b,c \} = \{ b \} \cup \{ c \} $$
The entire set X={a,b,c} can be obtained by uniting all sets in B, namely {a}, {b}, and {c}. $$ \{ a,b,c \} = \{ a \} \cup \{ b \} \cup \{ c \} $$

Thus, B serves as a basis for the topology on X because it allows us to construct all open sets in T through unions of sets in B.

Note. This example shows how different bases can exist for the same topology, each providing a different way to "generate" the open sets of the topology through unions of basic sets.

Example 2

The set comprising all real intervals (a,b) where a<b spans the entirety of the line.

$$ B=\{ \ (a,b) ⊂ \ R \ | \ a < b \ \} $$

This set serves as a basis because every point on the line can be found within an open interval (a,b).

Moreover, if two open intervals intersect, the point lying at the intersection is included in another set of B within that intersection.

For instance, considering two open intervals (0, 3) and (2, 4), their intersection is the open interval (2,3).
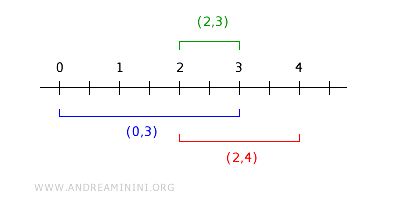
example of intersection between open intervals
The interval (2,3) in turn represents another set B_i within the basis B and is located within the intersection. $$ (0,3) \cap (2,4) = (2,3) ∈ B_i ⊂ (0,3) \cap (2,4) ⊂ B $$

Countable Basis

A countable basis for a topology on a space $ X $ is a "countable collection" of open sets $ \mathcal{B} = \{B_1, B_2, B_3, \dots\} $ such that every open set in $ X $ can be expressed as a union of elements from $ \mathcal{B} $.

A set is said to be "countable" if it either contains finitely many elements, or if its elements can be placed in one-to-one correspondence with the natural numbers $ \mathbb{N} $.

In other words, a collection is countable if its elements can be indexed as $ B_1, B_2, B_3, \dots $.

What's the difference between a basis and a countable basis?

In general, any basis generates the topology, but only those with "few enough" sets in the countable sense qualify as countable bases.

Why is this important? Having a countable basis is a valuable property in topology. For instance, it's one of the conditions in Urysohn’s Metrization Theorem. Moreover, many results in analysis and topology become more manageable or only apply in spaces with a countable basis.

Example

In $ \mathbb{R} $ equipped with the standard topology, the collection of open intervals $ (a, b) $ where $ a, b \in \mathbb{Q} $ (the rational numbers) and $ a < b $, forms a countable basis.

This is because we can list all such intervals in sequence - labeling them as I₁, I₂, I₃, and so on.

Proof

The set of natural numbers is countable because we can list them sequentially:

\[ 1,\ 2,\ 3,\ 4,\ 5,\ \dots \]

If we can similarly list all intervals $ (a, b) $ with rational endpoints and $ a < b $, then that collection is also countable.

Even though the rationals are infinite, they are countable. For example, we can arrange them as follows:

\[ 0,\ 1,\ -1,\ \tfrac{1}{2},\ -\tfrac{1}{2},\ \tfrac{2}{3},\ -\tfrac{2}{3},\ \dots \]

Let’s denote them $ q_1, q_2, q_3, \dots $

Now consider all pairs $ (q_i, q_j) $ such that $ q_i < q_j $.

For example:

$ (q_1, q_2) = (0, 1) $
$ (q_3, q_2) = (-1, 1) $
$ (q_4, q_5) = (\tfrac{1}{2}, -\tfrac{1}{2}) $ ❌ discarded because $ a > b $
$ (q_5, q_1) = (-\tfrac{1}{2}, 0) $
...

Each valid pair (i.e., those with $ a < b $) defines an open interval.

So we can list them in sequence:

$ (0, 1) $
$ (-1, 1) $
$ (-\tfrac{1}{2}, 0) $
$ (0, \tfrac{1}{2}) $
$ (-1, \tfrac{1}{2}) $
$ (\tfrac{1}{2}, 1) $
$ (-\tfrac{2}{3}, 0) $
$ (0, \tfrac{2}{3}) $
$ (-1, \tfrac{2}{3}) $
$ (-\tfrac{1}{2}, \tfrac{1}{2}) $
...

In short, even though there are infinitely many such intervals, they can be listed in order, just like the natural numbers. That’s precisely what it means for a set to be countable.

Hence, the collection of intervals $ (a, b) $ with rational endpoints and $ a < b $ is countable because we can enumerate them exhaustively, without omission - just as we do with the sequence 1, 2, 3, …

Observations

Some additional observations on the basis of a topology

If we consider a set X and construct a basis B in which every element x∈X is a set {x}∈B in the bases, we can form the basis of any topology T on the set X.
Generally, the union of singletons allows us to derive any topology.

For example, the basis B={ {a}, {b}, {c} } for the set X={a,b,c} generates the topology T={Ø,{a},{b,c},X}

The same basis B can generate any other topology on X like the topology T={Ø,{b},{a,c},X}, the trivial topology T={Ø, X}, or the discrete topology T={Ø,{a},{b},{c},{a,b},{a,c},{b,c},X}, etc.
Note. The first condition is met because every element of X is found in a set of B. The second condition is also met because the sets {x} are disjoint by construction, each being composed of a single element from the set X.

And so on.