Improper Subsets
What Are Improper Subsets
Improper subsets are defined as sets that are equal to themselves and the empty set.
Every set A always has two improper subsets:
- a set identical to itself $$ A = A $$
- the empty set $$ Ø ⊂ A $$
Equal Sets
Consider two equal sets (A=B)
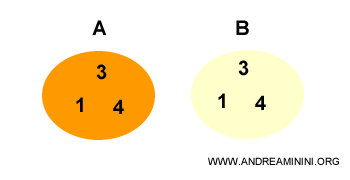
Every element of set A is also contained in set B.
Thus, A is a subset of B
$$ A ⊆ B $$
Similarly, every element of set B is contained in set A
Thus, B is a subset of A
$$ B ⊆ A $$
This particular reciprocal relationship implies equality between the sets
Therefore, when two sets are equal (A=B), each set is a subset of the other.
In these instances, we speak of improper subsets because A and B are not proper subsets of each other.
Note. A subset A is called a proper subset of B if all elements of A also belong to B but there is at least one element in B that does not belong to A. This situation does not occur when the sets are equal.
Example
Set A is included in set B and vice versa
$$ A = \{ 1,3,4 \} $$
$$ B = \{ 1,3,4 \} $$
Every element of set A is also an element of set B and every element of set B is also an element of A.
Therefore, the two sets are improper subsets of each other.
The Empty Set
A set is called the empty set if it does not contain any elements.
It is denoted by the symbol Ø. $$ Ø = \{ \ \ \} $$
The empty set is an improper subset of any other set.
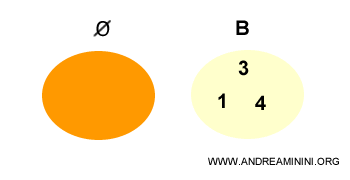
Note. The fact that the empty set is a subset of all other sets is a counterintuitive concept but provable (see proof). In the next example, I will try to explain it.
Example
Consider the empty set and a generic set A
$$ Ø = \{ \ \ \} $$
$$ A = \{ 1,3,4 \} $$
The empty set Ø is strictly included in set A
$$ Ø ⊂ A $$
To prove this, consider the opposite hypothesis to be false by contradiction.
"The empty set is NOT a subset of A"
Then there should be at least one element of the empty set that does not belong to set A.
However, this is a contradiction because the empty set has no elements.
Therefore, the statement "The empty set is NOT a subset of A" is false.
If this last statement is false, then the contrary statement "The empty set is a subset of A" is true.
Alternative Proof. The union of a set A with any of its subsets B⊆A equals the set itself. $$ A \cup B = A $$ The same applies to the union of a set and the empty set $$ A \cup Ø = \{ 1,3,4 \} \cup \{ \ \ \} = \{ 1,3,4 \} = A $$
