Complement of a Set

If set B is a subset of set A $$ B⊆A $$, the relative complement of B with respect to A is a set consisting of all elements of A that do not belong to B. $$ A \text{ \ } B = \{ x \in A | x \notin B \} $$ It is also referred to as the relative complement of B in A.

This is read as "the set A\B is the complement of set B" or "A\B is the relative complement of B in A".

Here is the Venn diagram.

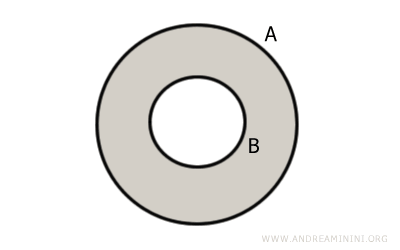
The gray area represents the complement of B in A, that is, the set A\B.

The complement coincides with the difference set A-B.

A Practical Example

Consider two finite sets A and B

$$ A = \{ 2, 4, 6, 8, 10 \} $$

$$ B = \{ 4, 6 \} $$

The complement of B with respect to A consists of elements in A that do not also belong to B

$$ A \text{ \ } B = A-B = \{ 2, 8, 10 \} $$

The graphical representation using Euler-Venn diagrams is as follows

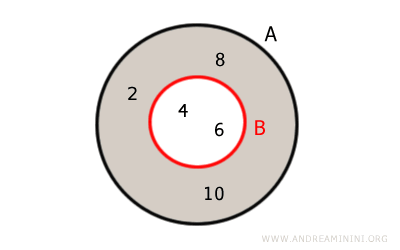
Explanation. The elements 4, 6 are common to both sets A and B. They are the elements shared between the two sets. The complement of B in A consists of the non-shared elements of A, which are { 2, 8, 10}.

Example 2

In this example, I consider two infinite sets.

The set of natural numbers N={1,2,3,4,5,...} and the subset of even natural numbers P={2,4,6,8,...}.

$$ N = \{ 1, 2, 3, 4, 5, ... \ \} $$

$$ P = \{ 2, 4, 6, 8, ... \ \} $$

The complement of P with respect to N is the set of odd natural numbers D

$$ N \text{ \ } P = D = \{ 1, 3, 5, 7, 9, ... \ \} $$

Absolute Complement

The absolute complement of a set A with respect to the universal set U is the set of all elements of U that do not belong to A. $$ C_A = \{ x \in U | x \notin A \} $$ It is also called the absolute complement of A.

What is the universal set?

The universal set U is the set that includes all sets being considered.

If not specified otherwise, the universal set is the set that includes all sets in general (universal set).

Example

Consider a set A within the universal set U

The complement of A, that is C_A (gray area), consists of all elements of U that do not belong to A (white area).

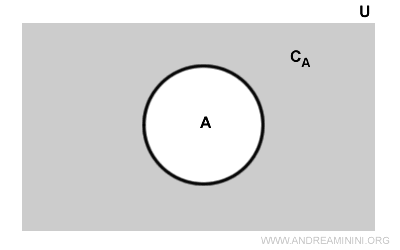
It is said "the set U\A (or U-A) is the complement of set A".

The complement U\A is also indicated with the notations U-A, C< sub>A, A^C, -A,

Observations

Some useful observations on complements

• The complement of A with respect to itself is the empty set because A-A=Ø.

  $$ A \text{ \ } A = A-A = Ø $$

• If A and B are equal sets A=B, the complement of B (or A) is the empty set.

  $$ A=B \Longleftrightarrow A-B = Ø $$

• The complement of the empty set with respect to set A is equal to A because A-Ø=A
  

  $$ Ø \text{ \ } A = A $$

• The union of set A and the complement of A with respect to B (that is, B\A) is the universal set B
  

  $$ A \cup (B \text{ \ } A) = B $$

• The intersection of set A and the complement of A with respect to B (that is, B\A) is the empty set
  

  $$ A \cap (B \text{ \ } A) = Ø $$

And so on.