Subsets

A set A is considered a subset of B if every element of A is also an element of B.

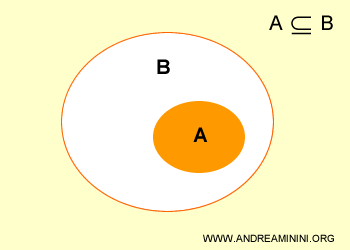
The graphical representation of sets shown above is known as a Venn diagram.

Put simply, subset A is contained within set B.

This relationship is referred to as inclusion.

To denote normal inclusion, the symbol ⊆ is used.

It reads as "set A is contained within set B".

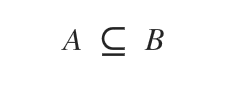
Other ways to interpret the above notation include "A is a subset of B" or "A is included in B".

The inclusion relationship can also be expressed as follows:

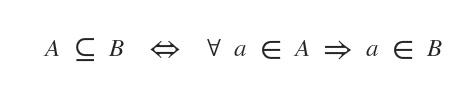
Note. The inclusion relationship also covers the case where A and B are identical sets, meaning they have the same elements and no different elements. Indeed, the symbol is a union of the inclusion symbol (⊂) and the equals symbol (=).

Proper Subset

A proper subset refers to when subset A is contained within set B, but there is at least one element in B that is not contained in A.

In simpler terms, the two sets are different A≠B.

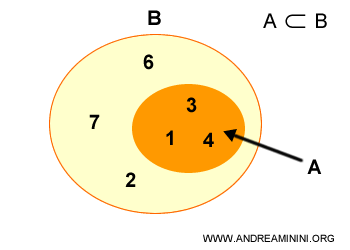
This situation is known as a strict inclusion relationship.

It's a specific type of inclusion, represented by the symbol ⊂.

It means "set A is a proper part of set B".

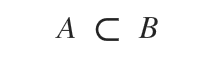
Alternatively, it can be said that "set A is strictly included in set B".

Example

Set A is strictly included in set B

$$ A = \{ 1,3,4 \} $$

$$ B = \{ 1,3,4,2,6,7 \} $$

Because every element of set A is also an element of B but there are elements in B that are not elements of A.

$$ A ⊂ B $$

What's the difference between normal inclusion and strict inclusion? In strict inclusion (A⊂B), the two sets A and B are always different (A≠B). In normal inclusion (A⊆B), however, the two sets can also be identical (A=B). Therefore, if strict inclusion (A⊂B) is true, then normal inclusion (A⊆B) is also true. $$ A⊂B \Longrightarrow A⊆B $$ Conversely, if normal inclusion (A⊆B) is true, it does not necessarily mean that strict inclusion (A⊂B) is true, because the two sets could be identical (A=B).

Improper Subset

Every set always has two improper subsets:


• a set identical to itself
• the empty set

A] The set identical to itself

When two sets are equal (A=B), each set is a subset of the other.

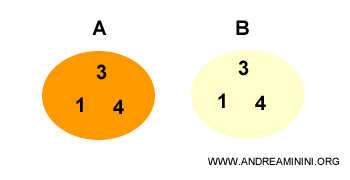
Because A contains every element of B and B contains every element of A.

In this case, it is said that:

• A is an improper subset of B
• B is an improper subset of A

This particular relationship of mutual implication implies equality between the sets.

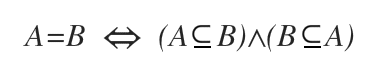
Therefore, when two sets are equal, they are also improper subsets of each other.

Example

Set A is included in set B and vice versa

$$ A = \{ 1,3,4 \} $$

$$ B = \{ 1,3,4 \} $$

Because every element of set A is also an element of B and every element of set B is also an element of A.

Thus, the two sets are equal (A=B).

B] The empty set

The empty set is considered an improper subset of any other set.

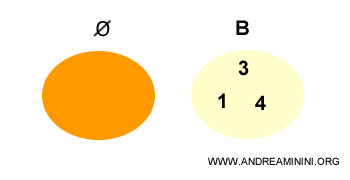
An empty set is defined as a set that has no elements.

It is represented by the symbol Ø. $$ Ø = \{ \ \ \} $$

Note. The concept that the empty set is considered a subset of all other sets might be initially challenging to grasp, but it can be demonstrated (see proof).

Example

Consider the empty set and any set A.

$$ Ø = \{ \ \ \} $$

$$ A = \{ 1,3,4 \} $$

The empty set Ø is also strictly included in set A

$$ Ø ⊂ A $$

Because the opposite cannot be claimed.

Proof. The proof is obtained by contradiction by assuming the opposite hypothesis. If the empty set were NOT a subset of A, then there would have to be at least one element in the empty set that does not belong to set A. However, this is impossible because the empty set has no elements. Therefore, if the statement "the empty set is not a subset of A" is false, then the contrary statement "the empty set is a subset of A" is true. Alternative proof. The union of a set A with one of its subsets B⊆A is always equal to the set itself. $$ A \cup B = A $$ The same occurs with the union of a set and the empty set $$ A \cup Ø = \{ 1,3,4 \} \cup \{ \ \ \} = \{ 1,3,4 \} = A $$

Singleton

What is a singleton?

A singleton is a subset that contains only one element.

Example

The subset B is a singleton because it is a subset ( B⊂A ) and contains only one element.

$$ A = \{ 1, 2, 3, 4, 5\} $$

$$ B = \{ 2 \} $$

Difference Between Inclusion and Membership

It's important not to mix up the concepts of inclusion and membership.

• The inclusion relation ⊆ is used exclusively among sets. It's applied to indicate that set A is a subset of B. $$ A \subseteq B $$
• The membership relation ∈ is employed solely between elements and a set. It serves to declare that one or more elements, a, b, are part of set A. $$ a \in A $$

Note: The same principle applies to the relations of non-inclusion and non-membership (∉). $$ a \notin A \\ A \nsubseteq B $$

Notes

Additional insights and observations about subsets.

• The Number of Subsets in a Set with \( n \) Elements
  A set with \( n \) elements has exactly \( 2^n \) subsets. This follows from the fact that each element in the set has two possibilities: it can either be included in a subset or left out.

  Example: If a set contains \( n = 3 \) elements, the total number of possible subsets is \( 2^3 = 8 \). Similarly, if the set has \( n = 4 \) elements, the number of subsets increases to \( 2^4 = 16 \).

 And so forth.