Proper Subsets

What Are Proper Subsets

A set A is called a proper subset of set B when


• every element of A is also in B
• at least one element of B is not in A.

This is referred to as a strict inclusion relationship.

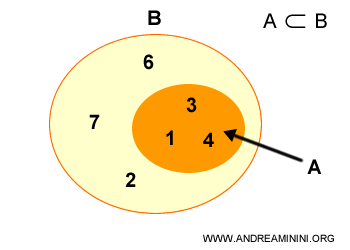
This is a specific case of inclusion, denoted by the symbol ⊂.

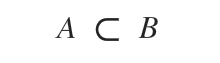
The latter statement is read as "Set A is a proper part of Set B" or "Set A is strictly included in Set B".

Strict inclusion implies that the two sets are different, A≠B.

What's the difference between normal inclusion and strict inclusion? In strict inclusion (A⊂B), sets A and B must be different (A≠B) because at least one element of B is not in A. Conversely, in normal inclusion (A⊆B), the sets can be the same (A=B). Thus, if strict inclusion (A⊂B) is true, then normal inclusion (A⊆B) is also true. However, if normal inclusion (A⊆B) is true, it does not necessarily mean that strict inclusion (A⊂B) is true, because the two sets could be the same (A=B).

Example

Set A consists of three elements, while Set B consists of six elements.

$$ A = \{ 1,3,4 \} $$

$$ B = \{ 1,3,4,2,6,7 \} $$

The first condition for strict inclusion is met because all elements of Set A are also in Set B.

$$ A = \{ 1,3,4 \} ⊂ B $$

The second condition is also met because there is at least one element in B that is not in A

In this case, there are three elements {2,6,7} in B that are not in A

$$ B = \{ 1,3,4,\color{red}2,\color{red}6,\color{red}7 \} $$

Therefore, Set A is strictly included in Set B, meaning Set A is a proper subset of B

$$ A ⊂ B $$

And so on.