Set Operations

Set operations include union, intersection, and difference.

To clarify the definitions of set operations, this page primarily uses Venn diagrams because they make understanding these operations easier. In graphical representation, concepts are much simpler compared to mathematical notation.

Union

Given two sets A and B, the union of A and B is the set containing all elements that are in set A, in set B, or in both.

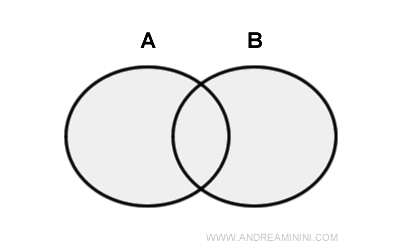
The symbol for union is ∪.

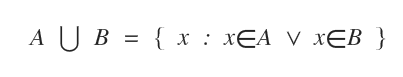
Any elements that are present in both sets are considered only once in the union set.

Union of multiple sets. To write the union of a family of sets, I can write $$ \bigcup_{i \in I} = \{ x \in A_i \:\: \text{for some}\:\: i \in I \} $$

How to calculate the union of two sets

In this practical example, I calculate the union of two sets A and B.

Explanation. Set A consists of the elements { 2, 5, 6, 7, 8 } while set B consists of the elements { 1, 3, 4, 6, 7, 9 }. The union set consists of elements from both sets { 1, 2, 3, 4, 5, 6, 7, 8, 9 }. Elements present in both sets {6, 7} are considered only once in the union set.

Intersection

Given two sets A and B, the intersection of A and B is the set containing all elements common to both sets A and B.

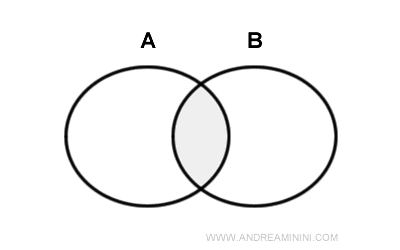
The symbol for intersection is ⋂.

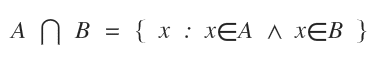
Two sets A and B are said to be disjoint sets when their intersection A⋂B is an empty set.

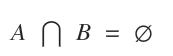
Intersection of multiple sets. To write the intersection among a family of sets, I can write $$ \bigcap_{i \in I} = \{ x \in A_i \:\: \forall i \in I \} $$

How to calculate the intersection of two sets

In this practical example, I calculate the intersection between two sets A and B.

Explanation. The elements { 6, 7 } belong to both set A and set B. Therefore, the intersection set A⋂B consists of the elements { 6, 7 }.

Difference between sets

Given two sets A and B, the difference A-B is the set containing elements of set A that are not also in set B.

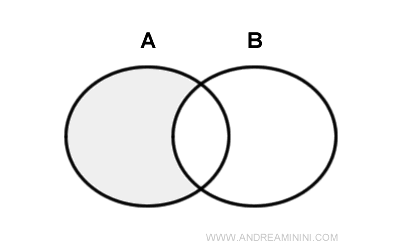
The set difference A-B is also called the complement of B with respect to A.

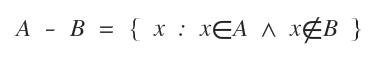
Note. The set difference A-B is also referred to as the relative complement of set A in set B. It includes all elements of A that are not also in B. It is often denoted as $$ A \text{ \ } B =\{ x \in A | x \notin B \} $$

How to calculate the difference between two sets

In this practical example, I calculate the difference between set A and B.

Explanation. Set A consists of the elements {2, 5, 6, 7, 8}. The elements { 6, 7 } belong to both set A and set B. Therefore, they are removed from the complement set A-B {2, 5, 6, 7, 8}. For this reason, the complement set A-B consists only of the elements {2, 5, 8}.

Properties of Set Operations

Set operations adhere to the following properties: commutative, associative, distributive, and De Morgan's Laws.

• Commutative Property

  A ∪ B = B ∪ A
  A ∩ B = B ∩ A

• Associative Property

  A ∪ (B ∪ C) = (A ∪ B) ∪ C
  A ∩ (B ∩ C) = (A ∩ B) ∩ C

• Distributive Property

  A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
  A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

• De Morgan's Laws

  A - (B ∪ C) = (A - B) ∩ (A - C)
  A - (B ∩ C) = (A - B) ∪ (A - C)