Identical Sets

Two sets A and B are identical sets (equal sets) if they satisfy the condition of mutual inclusion $$ A \subseteq B \wedge B \subseteq A $$ In this case, it is written $$ A = B $$

In simpler terms, two sets A and B are identical if A includes B and B includes A.

Both sets are improper subsets of each other.

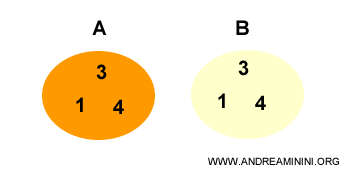
Proof

According to the first inclusion, all elements of set A belong to set B.

$$ A \subseteq B $$

Therefore, there are no elements in A that are not also contained in B.

According to the second inclusion, all elements of set B belong to set A.

$$ B \subseteq A $$

Thus, there are no elements in B that are not also contained in A.

If there are no elements in B not contained in A and no elements in A not contained in B, it is clear that the two sets are identical.

$$ A = B \Leftrightarrow A \subseteq B \wedge B \subseteq A $$

Alternatively, you could also say that two sets are equal when every element of A belongs to B and vice versa. $$ A = B \Leftrightarrow ( x \in A \Leftrightarrow x \in B ) $$

Example

I have two sets

$$ A = \{ 0, 1, 2, 3, 4 \} $$

$$ B = \{ x \in N \ | \ 2x + 1 < 10 \} $$

The second set B includes all natural numbers that meet the condition 2x+1<10.

$$ 2x+1<10 $$

$$ x < \frac{9}{2} $$

namely the natural numbers 0, 1, 2, 3, 4

$$ A = \{ 0, 1, 2, 3, 4 \} $$

$$ B = \{ 0, 1, 2, 3, 4 \} $$

As can be seen, both conditions of inclusion are satisfied

$$ A \subseteq B $$

$$ B \subseteq A $$

Therefore, the two sets are identical.

$$ A=B $$

Observations

A few notes on equal sets:

• Equal sets have identical cardinalities.
  Although it may seem straightforward, it's useful to remember. Since equal sets A = B contain the same elements, they also share the same number of elements, i.e., they have identical cardinalities. $$ | A | = |B| $$

And so forth.