Mathematical Relations

What is a Relation?

A relation is a rule that associates some element(s) of set A with one or more elements of set B. $$ aRb $$ Where a∈A and b∈B, and the element b is known as the image of a.

It's important to note that I used "some" because the rule does not have to apply to all elements of set A.

Similarly, it's not required to involve all elements of set B either.

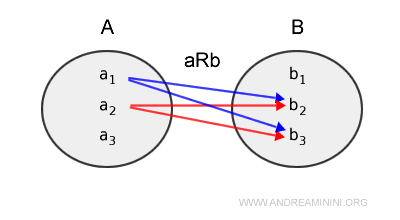
An element of set A can also relate to multiple elements of set B.

The previous Venn diagram can also be represented in the following way

Therefore, a relation is a subset of the Cartesian product AxB between the two sets.

$$ R \subseteq AxB $$

Note. When set A is equal to set B, that is, A=B, the mathematical relation is said to be defined on A.

A Practical Example

I have two sets A and B

$$ A = \{ 2, 4, 6, 8 \} \\ B = \{ 1, 3, 5 \} $$

The Cartesian product AxB is the set formed by all pairs (a,b) where a∈A and b∈B.

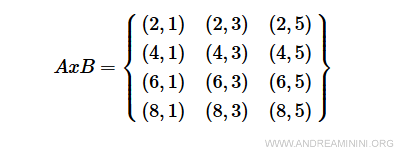
I have a relation R that identifies pairs of elements (a,b) such that a+2b<10.

For instance, the pair (a,b)=(2,1) satisfies relation R because 2+2·1=4<10

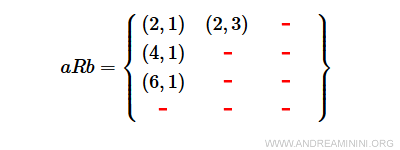
Note. The pair of elements (a,b) belongs to the Cartesian product of sets AxB. For this reason, a relation is a subset of the Cartesian product of sets.

The relation R identifies only a subset of the Cartesian product AxB

The pairs (2,1), (2,3), (4,1), and (6,1) satisfy relation R, while others do not.

Thus, the subset aRb consists of four elements.

$$ aRb = \{ (2,1), (2,3), (4,1) , (6,1) \} \subset AxB $$

Note. Of course, there are infinite relations between set A and B, and this is just one of many. For example, if relation R' is 2a+b<10, the subset aR'b is entirely different from the previous. $$ aR'b = \begin{Bmatrix} (2,1) & ( 2,3 ) & (2,5) \\ (4,1) & - & - \\ - & - & - \\ - & - & - \end{Bmatrix} $$

Example

Revisiting sets A and B and the relation R:a+2b<10

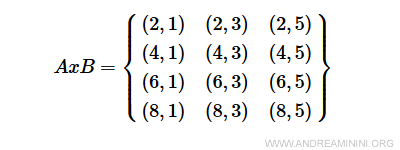
The elements of set A that satisfy the relation are 2, 4, 6

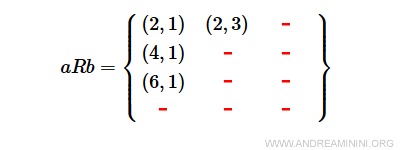
Therefore, the domain of R consists of elements 2, 4, 6 from set A and the codomain of R of elements 1, 3 from set B.

$$ \text{dom(R)} = \{2, 4, 6 \} $$

$$ \text{codom(R)} = \{1,3 \} $$

Note. In mathematics texts where the domain is the starting set A without distinguishing between elements that have or do not have an image in B through relation R, the domain consists of all elements of A. $$ \text{dom(R)} = \{2, 4, 6, 8 \} $$ In this case, the subset of A where relation R is actually defined is called the definition set or existence field of R. $$ \text{definition set} = \{2, 4, 6 \} $$

Representing a Relation

There are several ways to represent a binary relation between two sets:

• Enumeration Representation
  The ordered pairs (a;b) satisfying the relation are listed one after another $$ aRb = \{ (2;1), (2;3), (4;1), (6;1) \} $$
• Graphical or Arrow Diagram (or arrow diagram)
  It's the classic representation of a relation between two sets using an arrow that connects an element of set A to an element of set B.
  

  

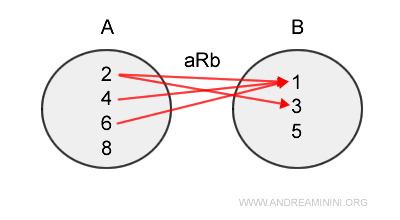
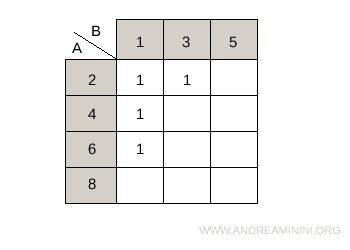
• Matrix of the Relation (or double-entry table)
  The relation can also be represented with a table, called the matrix of the relation, by placing elements a in rows and elements b in columns. In the cells where rows and columns intersect, insert
  • 1 if the pair (a,b) satisfies the relation R.
  • 0 if the pair (a,b) does not satisfy the relation R

  A practical example. The Cartesian product AxB is as follows:
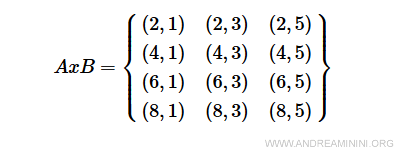
  To represent the relation aRb that meets the condition a+2b<10, I write the following relation matrix where the elements of the first set A are arranged vertically (rows) while those of the second set B horizontally (columns). $$ aRb = \begin{Bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{Bmatrix} $$ In a less mathematical but more understandable form, I can also represent the matrix through a double-entry table.
  

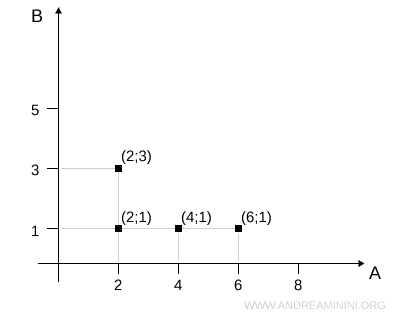
• Cartesian Graphical Representation
  In a Cartesian diagram, elements of the first set (domain) are placed on the horizontal axis, while those of the second set (codomain or image) on the vertical axis. Points on the plane indicate the ordered pairs (a;b) that satisfy the relation.
  

The Inverse Relation

Given a relation b=R(a), the inverse relation a=R^-1(b) connects elements b of set B to elements a of set A.

An inverse relation bR^-1a exists if and only if the relation aRb exists.

$$ bR^{-1}a \Leftrightarrow aRb $$

Therefore, the domain of the inverse relation R^-1 matches the codomain of the relation R

$$ dom \ R^{-1} = codom \ R $$

Moreover, the codomain of the inverse relation R^-1 matches the domain of the relation R.

$$ codom \ R^{-1} = dom \ R $$

A practical example

Revisiting sets A and B and the relation R:a+2b<10

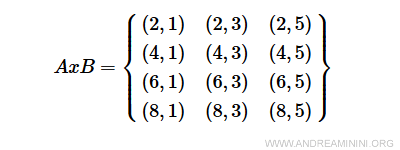
The elements of set A that satisfy the relation are 2, 4, 6

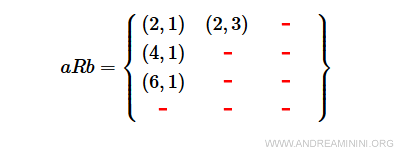
The relation from A to B is as follows

$$ aRb = \{ (2,1), (2,3), (4,1) , (6,1) \} \subset AxB $$

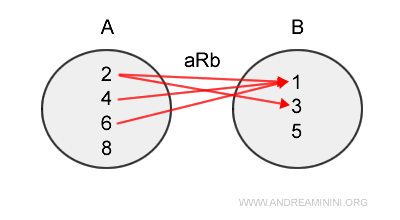
The inverse relation from B to A is as follows

$$ bR^{-1}a = \{ (1,2), (3,2), (1,4) , (1,6) \} \subset BxA $$

The direction of the inverse relation is opposite to the previous one.

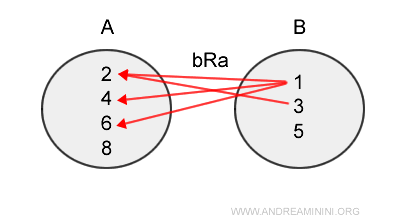
Note. In the aRb relation, pairs are (a,b). In the inverse relation, pairs are in reverse order, i.e., (b,a).

Types of Relations

There are three types of relations:

• Functions (applications)
• Binary Relations
  A binary relation between two sets A and B is a subset of the Cartesian product AxB. It is denoted by $$ aRb \ \ a \in A \ \ b \in B $$ It's called a binary relation because it relates elements of two sets. The binary relation generates pairs of elements (a;b) $$ (a;b) \in aRb $$
• Order Relations
  These are reflexive, antisymmetric, and transitive relations.
• Equivalence Relations
  These are reflexive, symmetric, and transitive relations.
• Compatibility Relations
  These are reflexive, symmetric, non-transitive relations.

Each type of relation has unique properties that distinguish it from the others.

• A relation is reflexive if $$\forall a \in A \Rightarrow (a,a) \in R $$
• A relation is symmetric if $$ \forall (a,b) \in R \Rightarrow (b,a) \in R $$
• A relation is antisymmetric if $$ \forall (a,b) \in R ∧ (b,a) \in R \Rightarrow a=b $$
• A relation is transitive if $$ \forall (a,b) \in R ∧ (b,c) \in R \Rightarrow (a,c) \in R $$

The properties of reflexivity, symmetry, and transitivity are independent of each other.

Therefore, there are relations where some properties are met and others are not.

The properties of a relation R from A to A are also met in the inverse relation R^-1 if the relation possesses any of the following properties: reflexive, symmetric, antisymmetric, transitive.

And so on.