Set Theory
Set theory is grounded in the use of the concept of a set within the logical-mathematical language.
Definition of a Set
A set is a collection of objects, known as elements or members, that share a specific property. It can also be referred to as a class, aggregate, or family.
This concept is primitive because it cannot be defined by referencing other concepts.
In a set, the order of the elements is not significant.
Definition of a Set in Mathematics
In mathematics, a set is a grouping of objects if there exists an objective criterion that determines whether any given object belongs to the grouping or not.
When discussing a mathematical set, it refers to a specific set where all objects meet an objective membership criterion.
Sets characterized by subjective criteria, on the other hand, are not considered mathematical sets.
From this point forward, when I mention "set," I am referring to mathematical sets.
Example. The set of prime numbers is a mathematical set because the membership criterion is objective. It includes all natural numbers divisible by 1 and themselves. $$ I = \{ 2 , 3, 5, 7, 11, ... \} $$ Conversely, the set of the best songs is not a mathematical set because the membership criterion is subjective. It varies from person to person.
Representation of Sets
In the logical-mathematical language, sets are denoted by uppercase letters (A, B, C, D, ...).
The elements of a set, however, are denoted by lowercase letters (a, b, c, d, ...).
Symbols of Membership and Non-membership
The symbol for belonging to a set is ∈.
It reads "element x belongs to set A".
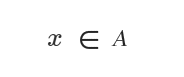
The symbol for not belonging to a set is ∉.
It reads "element x does NOT belong to set A".
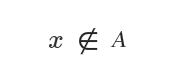
Example. Consider the set B of even numbers from 1 to 9. $$ B = \{ \ 2 \ , \ 4 \ , \ 6 \ , \ 8 \ \} $$ To indicate that the number 2 belongs to set B, write $$ 2 \in B $$ To indicate that the number 3 does NOT belong to set B, write $$ 3 \notin B $$
Graphical Representation
To graphically represent a set, Euler-Venn diagrams, also known as Euler circles, are used.
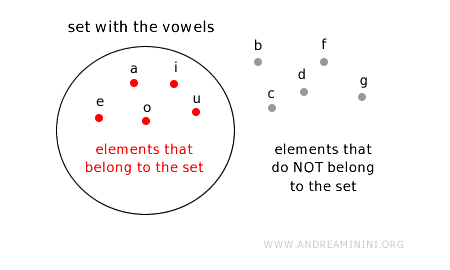
Each set is represented by a circle, an oval, or a closed polygon.
The elements that belong to the set are placed inside the circle.
Those that do not belong to the set are located outside the circle.
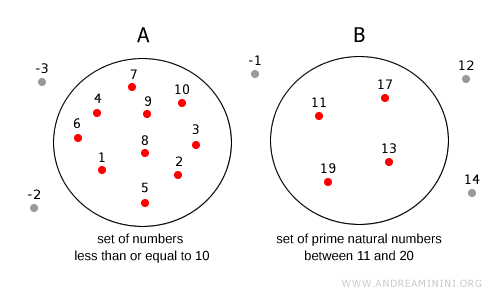
Note. In set A are the natural numbers up to 10. All numbers outside circle A do not belong to set A. In set B, however, are enclosed the prime numbers between 11 and 20. Similarly, all numbers found outside of circle B do not belong to set B. Numbers outside both circles (-1, -2, -3, 12, 14, ...) belong neither to set A nor to set B.
If an element belongs to both sets, it must be enclosed in both circles.
For example, if set B were the set of prime numbers between 1 and 20, I would have to represent sets A and B intersecting.
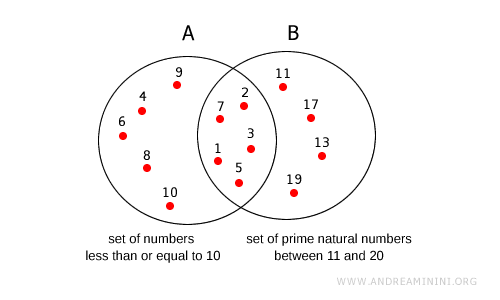
In this case, the elements common to both sets A⋂B={1, 2, 3, 5, 7} are enclosed in both A and B.
Note. Euler-Venn diagrams are named after the Swiss mathematician Leonhard Euler and the English mathematician John Venn who first used them to represent a set.
Tabular or Enumerative Representation
A very simple set can also be represented in a tabular manner.
In tabular representation, the elements belonging to the set are written within curly braces, separated by commas.
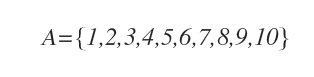
This representation is also known as enumerative notation.
It is not necessary to list the elements in any particular order. The order of elements is not important.
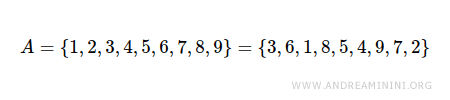
Any repeated elements within the set should be listed only once in the enumerative notation.
Therefore, there should be no repeated elements among the curly braces.
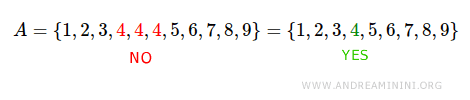
The tabular representation is handy when the set is finite and consists of a few elements.
It becomes cumbersome when the set has many elements.
Note. Dots ... are sometimes used when the membership rule to the set is clear enough, and the elements not explicitly listed are still implicitly understood. For example, A={1,2,...,10} means the natural numbers from 1 to 10. $$ A = \{ \ 1,2, \ ... \ ,10 \ \} $$ In tabular representation, dots ... are also used to indicate a set composed of infinite elements. For example, A={1,2,3,...} means all the natural numbers from 1 onwards. $$ A=\{ \ 1,2,3 \ ... \ \} $$
Set-builder Notation
A set can also be represented using set-builder notation, which is based on the rule or property of membership in the set.
This notation is useful if the set has many or infinite elements.
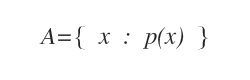
Within the curly braces, the rule of membership in the set, also known as the characteristic property, is indicated using the formal language of mathematical logic.
Example. In set-builder notation, the natural numbers from 1 to 10 are represented by A={x∈N:0<x≤10}.
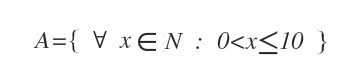
Where x is a variable that indicates any natural number x∈N. The symbol ∀ reads "for every". The colon : reads "such that". Sometimes the symbol | is also used to mean "such that". $$ A = \{ \ \forall \ x \in N \ | \ 0<x \le 10 \} $$ Therefore, the preceding notation reads as follows: "A is the set of natural numbers x such that x is a number between 0 and 10".
Pros and Cons of Notations
Set-builder notation can be used to represent any type of set, finite or infinite, as long as the elements can be identified by one or more criteria.
Enumerative notation, on the other hand, can only be used if:
- the set is finite and consists of a few elements
- the set is finite/infinite and can be represented by explicitly indicating only some elements and implying all others.
Finally, graphical notation is especially useful for explaining or visually communicating concepts that are otherwise difficult to grasp with logical-mathematical notation.
Finite and Infinite Sets
A set can be either finite or infinite.
- A finite set consists of a finite number n of elements.
Example. The set of books in a backpack is a finite set. Another example of a finite set is the set of sand grains in a container.
- An infinite set consists of an infinite number of elements.
Example. The set of natural numbers is an infinite set, as every natural number (n) has a successor (n+1). There is no natural number that is greater than all others.
Sets of Numbers
Sets of Numbers are sets composed of numbers
By convention, in mathematics, numerical sets are written with specific uppercase letters.
- N represents the set of natural numbers
- Z represents the set of integers
- Q represents the set of rational numbers
- I represents the set of irrational numbers
- R represents the set of real numbers
- C represents the set of complex numbers
The Empty Set
The empty set is a set without elements. It is denoted by the symbol Ø. $$ Ø = \{ \ \ \} $$
Sometimes the empty set is also indicated by two curly braces with no elements inside.
It's a special set because the empty set is a subset of any other set.
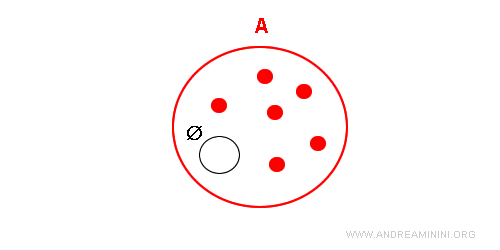
There is only one empty set. For example, the set of odd natural numbers divisible by two is an empty set because no odd natural number is divisible by two. Likewise, the set of squares with three sides is an empty set because every square has four sides. In both cases, it's the same empty set even though the criteria for membership differ.
And so on.
