Extremes of a Set

Defining the Extremes

In bounded sets, the extremities are finite numbers.
In unbounded sets, the extremities are represented by the symbols for plus or minus infinity (±∞).

A set might also be bounded above (having a finite supremum) while being unbounded below (infinite infimum), or the other way around.

Note: The supremum and infimum of a set may or may not be members of the set itself.

Delving into practical examples is beneficial for understanding the concepts of infimum and supremum.

The Infimum
The Supremum

The Infimum

For a set A and its subset B $$ B ⊆ A $$, the infimum of B is an element a∈A that is less than or equal to every element in b∈B. $$ inf(B) = a \le b \:\:\: a \in A, b \in B $$

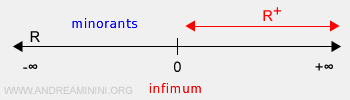
In bounded sets, the infimum is the highest among the lower bounds (minorants).

For instance, the infimum of B is the number 3.
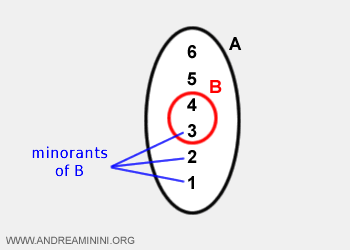
In unbounded sets, the infimum is negative infinity (-∞).

Example 1

Set A is the set of all real numbers R within the interval (-∞,+∞).

Set B is composed of 7 real numbers and is a subset of A.

$$ B = \{ 3, 4, 7, 5, 8, 9, 6 \} $$

The infimum of set B is the number three

$$ inf(B) = 3 \le b \:\:\: \forall \: b \in B $$

because the real number 3 is less or equal to all elements within set B.

Note: Here, the infimum inf(B)=3 is part of set B. However, it's not always the case.

Example 2

Set A is the set of all real numbers R within the interval (-∞,+∞).

Set B is the set of positive real numbers R⁺ and is a subset of A.

The infimum of set B is zero.

$$ inf(B) \le b \:\:\: \forall \: b \ \in \ B $$

It represents the greatest lower bound of the set R+.

Note: In this instance, the infimum inf(B)=0 does not belong to set B (R+) because there are infinitely many points between zero and any other positive real number.
the infimum example

The Supremum

For a set A and its subset B $$ B ⊆ A $$, the supremum of B is an element a∈A that is greater than or equal to every element in b∈B. $$ sup(B) = a \ge b \:\:\: a \ \in \ A \ , \ b \in B $$

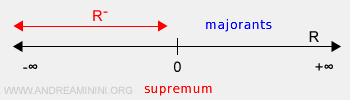
In bounded sets, the supremum is the lowest among the upper bounds (majorants).

For example, the supremum of B is 9.
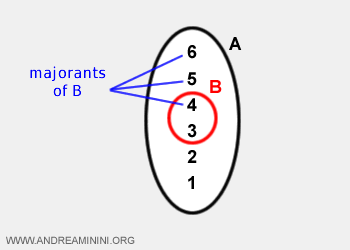
In unbounded sets, the supremum is positive infinity (+∞).

Example 1

Set A is the set of all real numbers R within the interval (-∞,+∞).

Set B comprises 7 real numbers and is a subset of A.

$$ B = \{ 3, 4, 7, 5, 8, 9, 6 \} $$

The supremum of set B is the number nine

$$ sup(B) = 9 \ge b \:\:\: \forall \: \ b \ \in B $$

because the real number 9 is greater or equal to all elements within set B.

Note: In this case, the supremum sup(B)=9 is part of set B. It's not a universal rule, though.

Example 2

Set A is the set of all real numbers R within the interval (-∞,+∞).

Set B is the set of negative real numbers R^- and is a subset of A.

The lower bound of set B is negative infinity.

$$ inf(B) = - \infty \le b \:\:\: \forall \: \ b \ \in B $$

Note: Here, the lower bound inf(B)=-∞ is part of set B (R^-) because the set of negative real numbers is unbounded below. Conversely, the upper bound sup(B)=0 is not part of set B (R^-) as it is not a negative real number.
an example of the supremum

And so forth.