Cartesian Product

The Cartesian product is an operation between two sets.

Definition

Given two sets A and B, the Cartesian product AxB is the set of all ordered pairs (a,b) where the first element "a" belongs to set A and the second element "b" belongs to set B.

In mathematical notation, the Cartesian product is defined as follows:

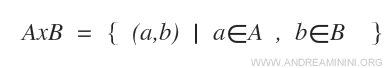
It is read as "A times B" or "A Cartesian B".

A Practical Example

For calculating the Cartesian product, I prefer to use a practical example.

Consider two sets A and B consisting of two and three elements, respectively.

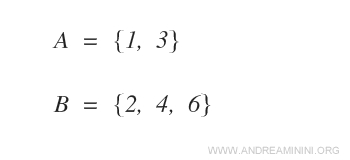
The Cartesian product AxB is the following set:

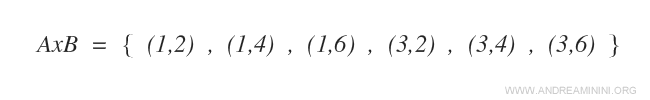
Every element of the Cartesian product set AxB is an ordered pair.

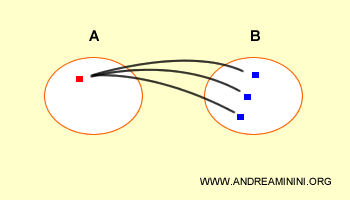
Graphically, the two sets are connected by these relationships.

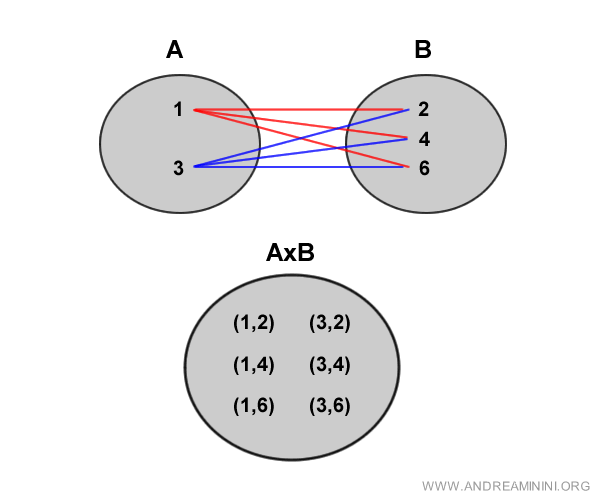
Note. The elements of the Cartesian product do not belong to sets A or B because they are of a different nature; they are pairs of elements from A and B.

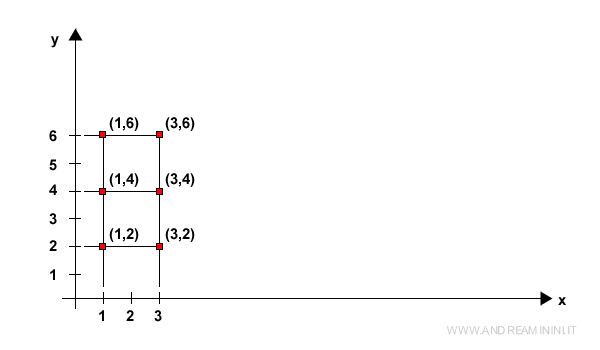
Ordered pairs of the Cartesian product can be represented as coordinates (x,y) on a Cartesian diagram.

Representing the Cartesian Product

The Cartesian product can be represented through:

• A Cartesian diagram
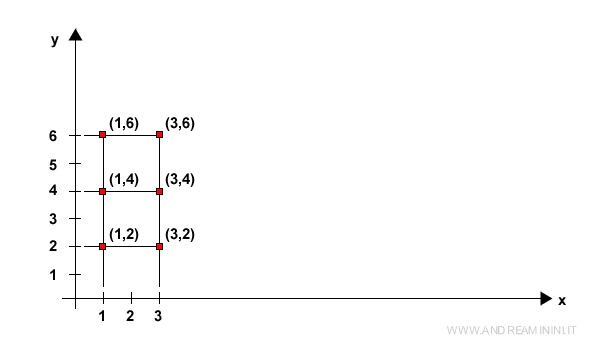
  I draw a Cartesian diagram indicating the elements of set A on the x-axis (horizontal axis) and those of set B on the y-axis (vertical axis). Each pair (a;b) from the Cartesian product (AxB) corresponds to a unique point on the Cartesian plane (x;y) where x=a and y=b.
  
• A double-entry table
  On the rows of the table, I indicate the elements of the first set (A) of the Cartesian product AxB. On the columns, I indicate the elements of the second set (B) of the Cartesian product AxB. In the cells of the table (or matrix), I insert the ordered pair (a;b) of the corresponding elements from the row and column.
  

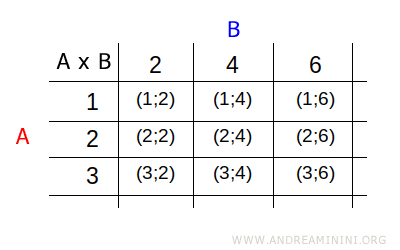
  Note. The tabular representation of the Cartesian product AxB is useful when the elements of one or both sets are not numbers.

• Tree Diagram
  The Cartesian product can be visualized as a tree, with the "root" representing the starting point. Each element of \( A \) branches out, creating new nodes. - From each node generated by \( A \), further branches extend, corresponding to elements of \( B \). - The terminal nodes of the tree (known as "leaves") represent the ordered pairs \((a, b)\) in the Cartesian product \( A \times B \).
  

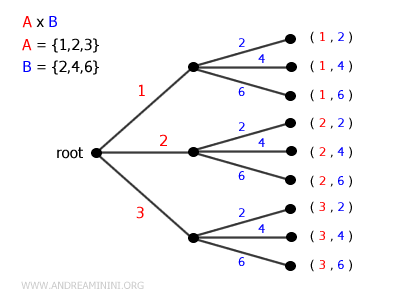
  Note. When this concept is extended to multiple sets \( A_1, A_2, \dots, A_k \), the tree deepens. At each level, the number of branches corresponds to the number of elements in the respective set. - The final leaves represent the ordered k-tuples \((a_1, a_2, \dots, a_k)\). This visualization is particularly useful in computer science for modeling search spaces, automata, and hierarchical data structures.

What is an Ordered Pair?

An ordered pair (a,b) is a pair of objects where a is the first element and b is the second element.

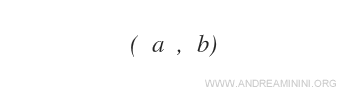
To indicate an ordered pair, parentheses are used with the elements separated by a comma.

The elements a and b do not necessarily have to be different.

The order of the elements is important

In an ordered pair, the order of the elements is crucial.

Example

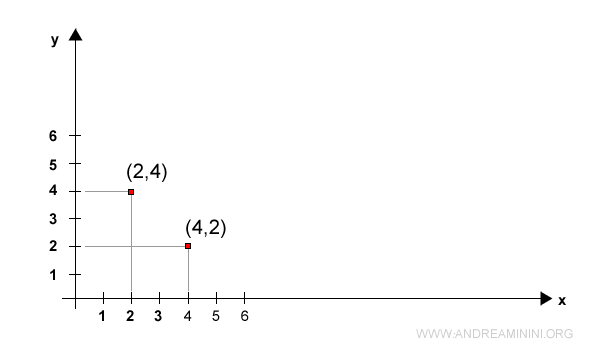
The ordered pairs (2,4) and (4,2) are different. They have the same values but in a different order.

The two ordered pairs indicate different coordinates on the Cartesian plane (x,y).

When are two ordered pairs equal?

Given two ordered pairs (a,b) and (c,d), the pairs are equal only when the first element of the first pair is the same as the first element of the second pair (a=c) and the second element of the first pair is the same as the second element of the second pair (b=d).

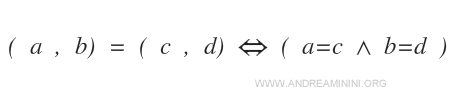
The Commutative Property of the Cartesian Product

The Cartesian product does not have the commutative property.

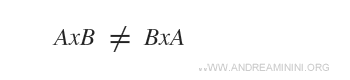
Example

 

 

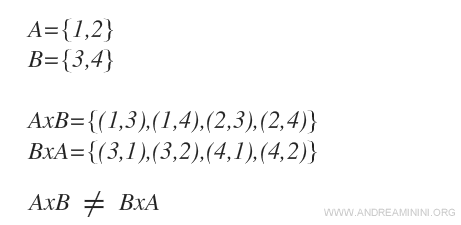
It is evident that AxB ≠ BxA because, unlike in a set, in an ordered pair the order of the elements is significant.

The difference is clear when representing the two Cartesian products on a Cartesian diagram.

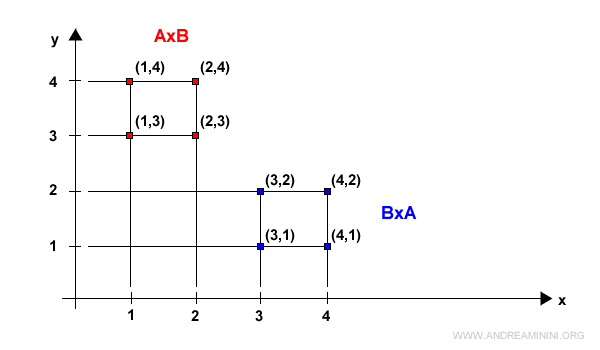
Note. The only case where AxB = BxA is when A=B. When the two sets A and B are identical, the Cartesian product respects the commutative property.

The Distributive Property

The Cartesian product between two sets respects the distributive property with respect to union and intersection.

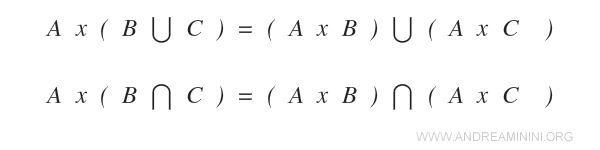
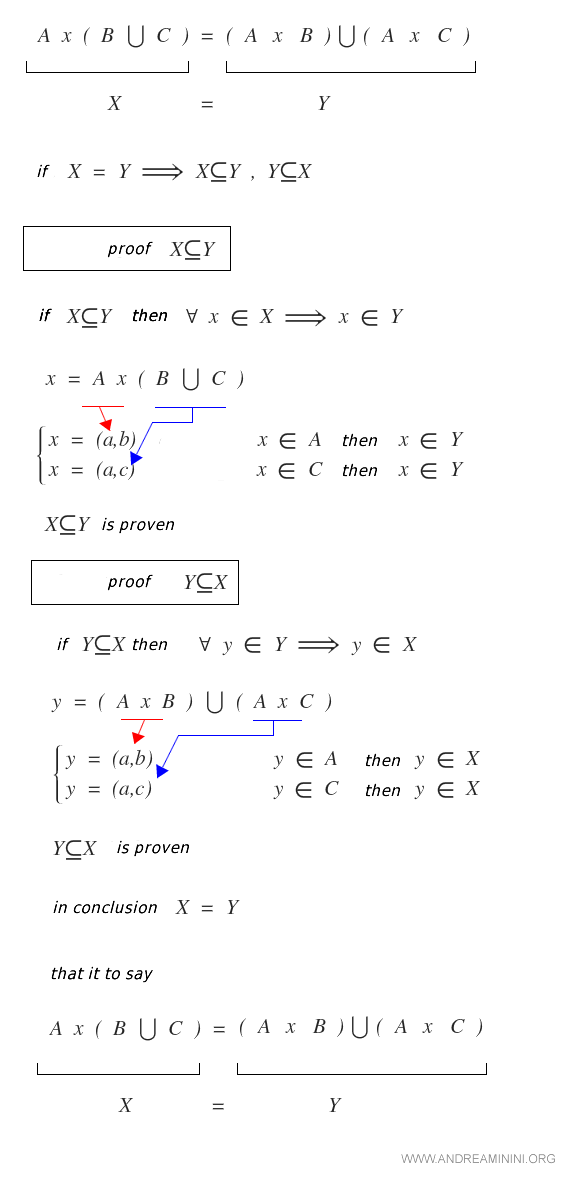
Proof

The Cartesian Product of n Sets

The Cartesian product is a fundamental operation that extends beyond just two sets—it can be applied to any number of sets.

Given \( n \) sets \( A_1, A_2, \dots, A_n \), their Cartesian product, denoted as \( A_1 \times A_2 \times \dots \times A_n \), is the set of all ordered \( n \)-tuples \( (a_1, a_2, \dots, a_n) \) where: $$ A_1 \times A_2 \times \dots \times A_n = \{ (a_1, a_2, \dots, a_n) \mid a_i \in A_i, \quad \forall i = 1,2,\dots,n \} $$

In other words, each coordinate of an ordered \( n \)-tuple is drawn from a corresponding set in the sequence.

More generally, when working with multiple sets, the elements of the Cartesian product are \( k \)-tuples (i.e., ordered sequences of \( k \) elements), where each component comes from a different set.

Example

Consider the following three sets:

$$ A = \{1,2\} $$

$$ B = \{a,b,c\} $$

$$ C = \{X,Y\} $$

Their Cartesian product is:

\[ A \times B \times C = \{ (1,a,X), (1,a,Y), (1,b,X), (1,b,Y), (1,c,X), (1,c,Y), (2,a,X), (2,a,Y), (2,b,X), (2,b,Y), (2,c,X), (2,c,Y) \} \]

The total number of elements in the Cartesian product is simply the product of the cardinalities of the individual sets:

\[ |A \times B \times C| = |A| \cdot |B| \cdot |C| = 2 \times 3 \times 2 = 12 \]

In this case, the Cartesian product consists of 12 ordered triples.

More generally, when forming the Cartesian product of multiple sets, the total number of resulting tuples is always given by the product of the sizes of the sets involved.

The Cartesian Product of a Set with Itself

The Cartesian product can also be applied to a set with itself.

Taking a set \( A \) and computing its Cartesian product with itself \( k \) times yields:

\[ A^k = A \times A \times \dots \times A \]

The elements of \( A^k \) are all possible ordered \( k \)-tuples consisting of elements from \( A \). If \( A \) contains \( n \) elements, then the number of elements in \( A^k \) is given by:

\[ |A^k| = n^k \]

Example

Consider the set:

$$ A = \{1,2,3\} $$

The Cartesian product \( A \times A \) consists of all possible ordered pairs:

$$ A \times A = \{ (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3) \} $$

Since \( A \) contains \( n = 3 \) elements, the number of ordered pairs in the Cartesian product is:

\[ |A^2| = 3^2 = 9 \]

Instead of writing \( A \times A \), it is common to use the notation \( A^2 \):

$$ A^2 = A \times A = \{ (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3) \} $$

The notation changes, but the meaning remains the same.

Example 2

Now consider the set \( A = \{0,1\} \) and let \( k = 3 \). The Cartesian product \( A^3 \) consists of:

\[ A^3 = A \times A \times A = \{ (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1) \} \]

Since \( A \) contains \( n = 2 \) elements, the number of ordered triples is:

\[ |A^3| = 2^3 = 8 \]

In general, this principle holds for any Cartesian product where a set is taken with itself \( k \) times.

Key Observations

• If a set \( A \) has \( n \) elements and a set \( B \) has \( m \) elements, then each element of \( A \) can be paired with each element of \( B \), yielding exactly \( n \cdot m \) ordered pairs. Therefore, the number of elements in \( A \times B \) is:

\[ |A \times B| = |A| \cdot |B| = n \cdot m \]

Note: This property generalizes to multiple sets. If we have \( k \) sets \( A_1, A_2, \dots, A_k \) with respective cardinalities \( n_1, n_2, \dots, n_k \), then their Cartesian product contains:

\[ |A_1 \times A_2 \times \dots \times A_k| = n_1 \cdot n_2 \cdot \dots \cdot n_k \]

This generalization is widely used in combinatorics, probability theory, and various branches of computer science, including state space exploration and relational databases.