Compact Set

More formally, in a topological space, a set \(K\) is compact if every open cover of \(K\) admits a finite subcover that still covers \(K\).

These definitions are equivalent in \(\mathbb{R}^n\), but they may differ in more general spaces.

Note. Compactness guarantees a number of powerful properties, such as ensuring that continuous functions attain both their maximum and minimum values (Weierstrass Theorem), and that from any sequence, a convergent subsequence can always be extracted (Bolzano - Weierstrass Theorem). In particular, if a function is continuous on a compact set, it will achieve its maximum and minimum values - with no exceptions.

Examples

Example 1

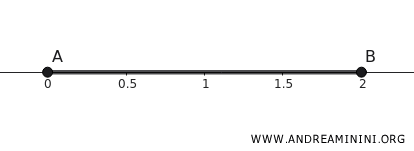
Consider the interval \([0,2]\) on the real number line \(\mathbb{R}\).

Define the set:

\[ K = \{ x \in \mathbb{R} \mid 0 \leq x \leq 2 \} \]

This set is compact because:

• It is closed: it contains the boundary points \(0\) and \(2\).
• It is bounded: all points lie between \(0\) and \(2\), so the set doesn't extend indefinitely.

Example 2

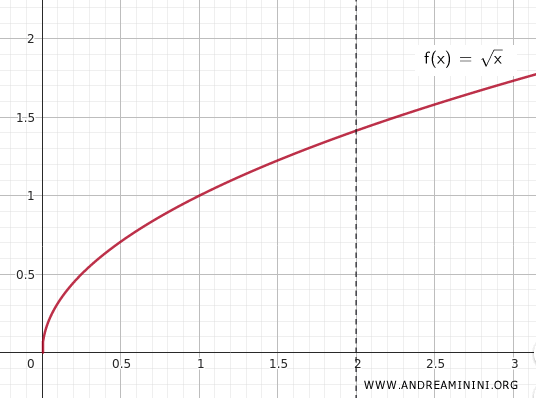
Now consider the continuous function \(f(x) = \sqrt{x}\) defined on \(K\).

Since \(f(x)\) is continuous on a compact set, by the Weierstrass Theorem, it must attain both a maximum and a minimum value on \(K\).

Indeed, over \([0,2]\), \(f(x)\) reaches its minimum at \(x = 0\) (value \(0\)) and its maximum at \(x = 2\) (value \(\sqrt{2}\)).

Example 3

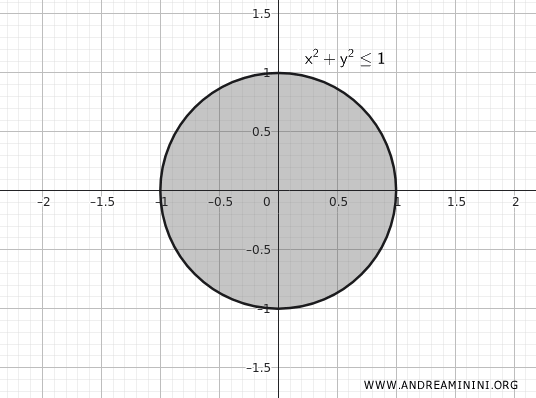
Next, consider the closed disk of radius \(1\) centered at the origin in the plane \(\mathbb{R}^2\).

Define the set:

\[ K = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 1 \} \]

This set is also compact because:

• It is closed: it contains all points on the boundary circle where \(x^2 + y^2 = 1\).
• It is bounded: no point lies more than a distance \(1\) away from the origin \((0,0)\).

And so on.