Distance Between Sets

The distance between two sets $A$ and $B$ in a metric space $(X, d)$ is defined as the smallest possible distance between any point in $A$ and any point in $B$. $$ d(A, B) = \inf \{ d(a, b) \mid a \in A \ , \ b \in B \}, $$ where $d(a, b)$ represents the distance between two points $a$ and $b$ according to the metric $d$, and $\inf$ (infimum) denotes the lowest value among all these distances.

To calculate the distance between two sets, you evaluate every possible pair of points—one from $A$ and one from $B$—and find the smallest distance among them.

The distance between the sets is the minimum of all these distances.

Note: The distance between sets indicates how close the points of the two sets can get, but it doesn’t necessarily mean the sets touch or are identical.

When the Distance is Zero

A distance of zero $d(A, B) = 0$ implies that points in $A$ and $B$ can come arbitrarily close, but it doesn’t necessarily mean the sets touch or share any points.

As a result, the distance can be $0$ even if the sets are disjoint, $A \cap B = \emptyset$.

A Practical Example

Let’s consider two sets $A$ and $B$ in a metric space consisting of all points on a line, with the distance defined as $d=|x_1-x_2|$.

We’ll analyze three distinct cases:

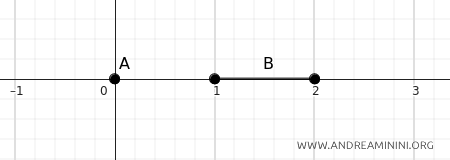
A] Case 1

If $A = \{0\}$ and $B = [1, 2]$, the distance between them on the number line is $1$.

$$ d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \} = d(0, 1) = 1 $$

Here, the point $0$ in $A$ is exactly $1$ unit away from the closest point in $B$, which is $1$.

example

B] Case 2

If $A = [0, 1]$ and $B = [1, 2]$, their distance is zero.

$$ d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \} = d(1, 1) = 0 $$

In this case, $A$ and $B$ "touch" at the point $1$, so the distance is $0$.

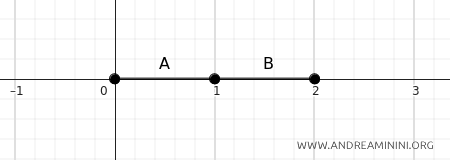
example

The two sets are not disjoint because their intersection is not empty:

$$ A \cap B = \{ 1 \} $$

C] Case 3

If $A = (0, 1)$ and $B = (1, 2)$, their distance is zero.

$$ d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \}. $$

Here, the two sets are disjoint because they are open intervals, and the point $1$ is not included in either $A$ or $B$... yet the distance is still zero.

$$ A \cap B = \emptyset $$

This occurs because, to minimize the distance, you can make $a$ approach $1$ (the right endpoint of $A$) and $b$ approach $1$ (the left endpoint of $B$) as closely as possible.

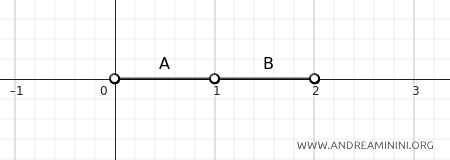
example

The point $a$ in $A$ can get arbitrarily close to $1$ but cannot reach it, since $A$ is an open interval.

Similarly, the point $b$ in $B$ can come arbitrarily close to $1$ but cannot reach it, as $B$ is also an open interval.

Therefore, the distance between $A$ and $B$ is:

$$ d(A, B) = \inf \{ |a - b| \mid a \in A, b \in B \} = |1 - 1| = 0 $$

In conclusion, even though $A$ and $B$ do not touch (i.e., they have no points in common), there are points in $A$ and $B$ that can get arbitrarily close to each other.

For this reason, the distance between $A$ and $B$ is $0$.

Note: Even if the distance between two sets is $0$, this doesn’t mean the sets are identical or that they touch. The concept of distance focuses on points getting arbitrarily close, not necessarily on direct contact.

And so on.